Tweet or Honk: Has Trump been Goosing the Markets with Social Media?
08 December 2020
Abstract:
In this post we use Trump’s Twitter data to predict whether market volatility (the VIX) will increase that day. To accomplish this we use a Natural Language Processing (NLP) bag-of-words approach with dimensionality reduction through truncated Singular Value Decomposition (SVD) for latent sentiment analysis. The predictions are decided by a weighted voting classifier ensemble consisting of hyperparameter tuned logistic regression, decision tree, random forest, Adaptive Boosting (AdaBoost) of decision trees, and stochastic gradient boosted decision tree models. To handle the large amounts of data we use Dask and sklearn’s joblib for parallel processing as well as sparse matrix data structures.
Background:
To say that President Trump has garnered public attention with his Twitter posts is a gross understatement; one need only look at the small fortunes being made selling ‘covfefe’ merch on the internet as an indicator of the rapt attention he holds both over his supporters and detractors alike. He is at the same time Jack Dorsey’s greatest enemy and his greatest asset by drawing the president’s personal ire for his actions and creating a mountain of ad-space revenue in one push of a blue button. Though Obama had a Twitter account as during his administration, it served as a more traditional and benign presence. Even before declaring his intentions to run for office in June of 2015 Trump communicated with Twitter in a way that was direct, unpolished, seemingly always irate, and at times obscene. Now it has become almost expected as a new standard: Can any future president really be seen as engaged with their constituency if their every unfiltered thought is not constantly being uploaded to the clout-cloud?
In this light it has become a common inside joke among investors that they live in constant fear of what his next Tweet will bring to the market. This is not to say other presidents and governmental actions have not affected the market. In an age where securities can be bought and sold in microseconds and a tweet can be shared with the general public before even the president’s own staff find out, there can seem to be some evidence for this claim.
Investors can however be a notoriously superstitious bunch; regardless of how many Fibonacci retracements and moving averages you want to throw in a chart, technical “analysis” has very little to do with quantitative mathematics and more to do with engagement (besides, backtesting reveals it is about as effective as flipping a coin). So how do we know if there is any merit to this claim?
To address the question of whether Trump has any power to affect markets with his use of social media we first need to look at our problem through a greater scope. In a perfectly efficient market both everyone and no one participating in the market has this power of influence to some roughly equal extent. Everyone has this power by their own valuations determining where they lie on the bid ask spread. At the same time no one has this power as it surpasses no one else’s ability to do the same, and if you have actual intentions of buying a product your bid needs to be at least reasonable. In reality, markets aren’t quite so efficient, and some people hold more sway over others. It only makes sense that a person that holds power over financial and fiscal policies would hold at least a little more of this power than others.
We must also consider where this information actually comes from. While Trump may be the author of the tweet, is he the originator of the idea that can cause changes in the market, or is he merely a conduit for that idea? He is, after all, an elective representative. Isn’t it logical that, to at least some extent, his tweets represent the opinions of a large segment of the market participants?
One might logically conclude that the market is more worried about the action that may follow a particular tweet than the tweet itself, but while policies are rigid and binding with an ability to set real limits on profits, tweets are quite the opposite. They are temporary documents of opinions that may change within minutes, and in general operate on a more “sell the rumor, buy the news” principle. If Trump’s tweets really have a consistent relationship with the markets we should expect to see spikes of volatility correlated to our tweet’s metrics. As implied volatility tends to overstate historical volatility, we should expect to see the most reaction to our tweet from volatility change rather than price movement of underlying assets. In addition, the VIX gives us an ability to get a two-sided perspective on volatility. Although it is usually associated with falling prices, a large spike in price can also drive volatility.
In this project we will use our data science tools to see to what extent, if any, Trump’s use of Twitter has on market volatility.
Computing Environment:
Python 3.7.0numpy 1.19.2
pandas 1.1.2
dask 2.30.0
dask-ml 1.7.0
yfinance 0.1.55
multiprocess 0.70.10
joblib 0.17.0
DateTime 4.3
matplotlib 3.3.2
seaborn 0.11.0
wordcloud 1.8.0
Pillow 7.2.0
scipy 1.5.3
contractions 0.0.25
nltk 3.5
scikit-learn 0.23.2
Data:
Twitter Data:
The following columns are derived from Donald Trump’s Twitter data relating to the verified account @realDonaldTrump.‘truncated’: This column indicates whether the tweet is truncated. A truncated tweet is a tweet that exceeds the maximum allowed characters for a tweet and is divided among two or more tweets with the use of an ellipsis at the end and beginning of the continuing tweets to indicate this to the user. A 1 indicates the tweet being part of a truncated body while a 0 indicates the entire message is in a single tweet.
‘text’: This column is a string containing all the words in the tweet, including emojis.
‘Is_quote_status’: This column indicates whether this tweet is a quote of another user’s tweet.
‘favorite_count’: This column counts how many other users have favorited this tweet.
‘retweeted’: This column indicates whether this tweet has been retweeted by other users. A 1 indicates that the tweet has been retweeted by other users. A 0 indicates the tweet has not been retweeted by other users.
‘retweet_count’: This column counts how many other users have retweeted this tweet.
Market Data:
^VIX: The CBOE Volatility Index used to measure forward-looking (implied) volatility. Calculated from the call to put ratio on 23 to 37 day options contracts on SPX.
Data sourcing and cleaning:
JSON files containing Trump’s Twitter data were sourced from https://github.com/bpb27/trump_tweet_data_archive. This data gives us all of Trump’s tweets up until July of 2017. Unfortunately, the code used to generate this data has become deprecated. I spent quite some time working with Selenium and BeautifulSoup to try and rectify this in addition to communicating with the publisher as well as other Github users who had commented on this same issue, but to know avail. It seems there are two main issues: the CSS selector has been changed to some very obscure location, and Twitter will stop your page requests after a few hundred pages even with a delay of five seconds between requests. I also tried to source the data directly from Twitter using the Tweepy API, but my free Twitter Developer Access only allows me to go a few thousand tweets back in time. For full access to a user’s newsfeed one would need to pay for a higher tier Twitter Developer Account, and would be the most likely plan of action were this to be deployed.
To establish proof of concept, we downloaded three JSON files from the Github archive for the years 2015, 2016, and 2017 (up to deprecation). As we loaded our unstructured JSON files into Pandas DataFrames, some columns became dictionaries containing what were other variables. Some of the data tracked by Twitter was added and removed throughout the years, so we rectify our files to only contain data that is also in the other years’ files. We drop all columns except for those mentioned in the data dictionary above.
Our next step takes into consideration when we define a day to be. If Trump tweets something after markets are closed, it obviously should not be counted as relating to that same calendar day. In respect to this we should set our ‘day’ to start and end at 4pm when markets close. Since our data is already in UTC (as all good data time series data is stored) and five hours ahead of Eastern Time, we shift all of our tweets three hours ahead so that 4pm Eastern time becomes our new ‘midnight’.
Our VIX data was scraped using the yfinance Yahoo Finance API. We retrieved all historical data for ^VIX closing prices. We then localized the time zone to UTC from a date only object. We next define a variable called ‘volatilityUp’ that is 1 if the volatility is as high or higher than the previous close and 0 if not. We chose to count volatility as up even if the price is exactly the same as it was the day before. This is because volatility inherently depreciates over time as front-end contracts are rolled out for more expensive later-dated contracts in addition to normal contract theta-decay. To put it simply, if there were no inherent risk-free rate in the market and volatility could grow in the long-term there wouldn’t be a market because no one would invest in it (at least in the long-term, people still buy lottery tickets). If volatility is at the same level today as it was yesterday despite these factors that is essentially a growth so we are going to count that as an up day (though the scenario where something closes at the exact same price as it did the day before almost never happens). After creating this column, we drop the original column that contained the closing prices so that we have only our ‘volatilityUp’ variable and our datetime index. If this model were to be scaled for deployment, there are paid data sources that can provide hourly, minute, and ticker level data.
After performing our initial data cleaning on our individual table we append each year’s DataFrame in consecutive order and delete duplicate rows to account for any overlap in file entries (there is overlap, so this is necessary). Next we merge our Twitter DataFrame with our VIX DataFrame with a full join. We drop all rows occurring before July 16th of 2015 to limit our data to after the day Trump announced his intentions to run for office. Since there is only one closing price per day and turning our VIX date object to a datetime object sets each close price at midnight of that day, we forward fill our ‘volatilityUp’ values to fill each tweet with the volatility outcome for that market day. We next drop all rows where our ‘text’ value is empty. We now have one remaining issue with our data. The Twitter historical data for a user contains not only tweets authored by that user, but all tweets that mention that user’s twitter handle. Luckily, these all appear with the same beginning format: @USERNAME: (where USERNAME would be filled by the tweet authors username). We use a simple Regex statement to filter these other users out.
Next we create some new variables from our text data. All-caps words indicate emphasis, and is widely seen as the internet equivalent to yelling. There are some common exceptions to this (USA, FOX, UK, and NAFTA to name a few), but a high presence of capitalized words may indicate heightened emotion, or personal volatility. We use a Regex statement to count the number of all-caps words per tweet. Exclamation points also indicate higher emotional levels in a message. We use a Regex statement to count the number of exclamation points per tweet. We count the total number of words in a tweet, as being able to fit a higher number of words within the same character limit indicates a high presence of shorter words. This may be an indicator of a tweet being written more impulsively with less thought put to the concept beforehand.
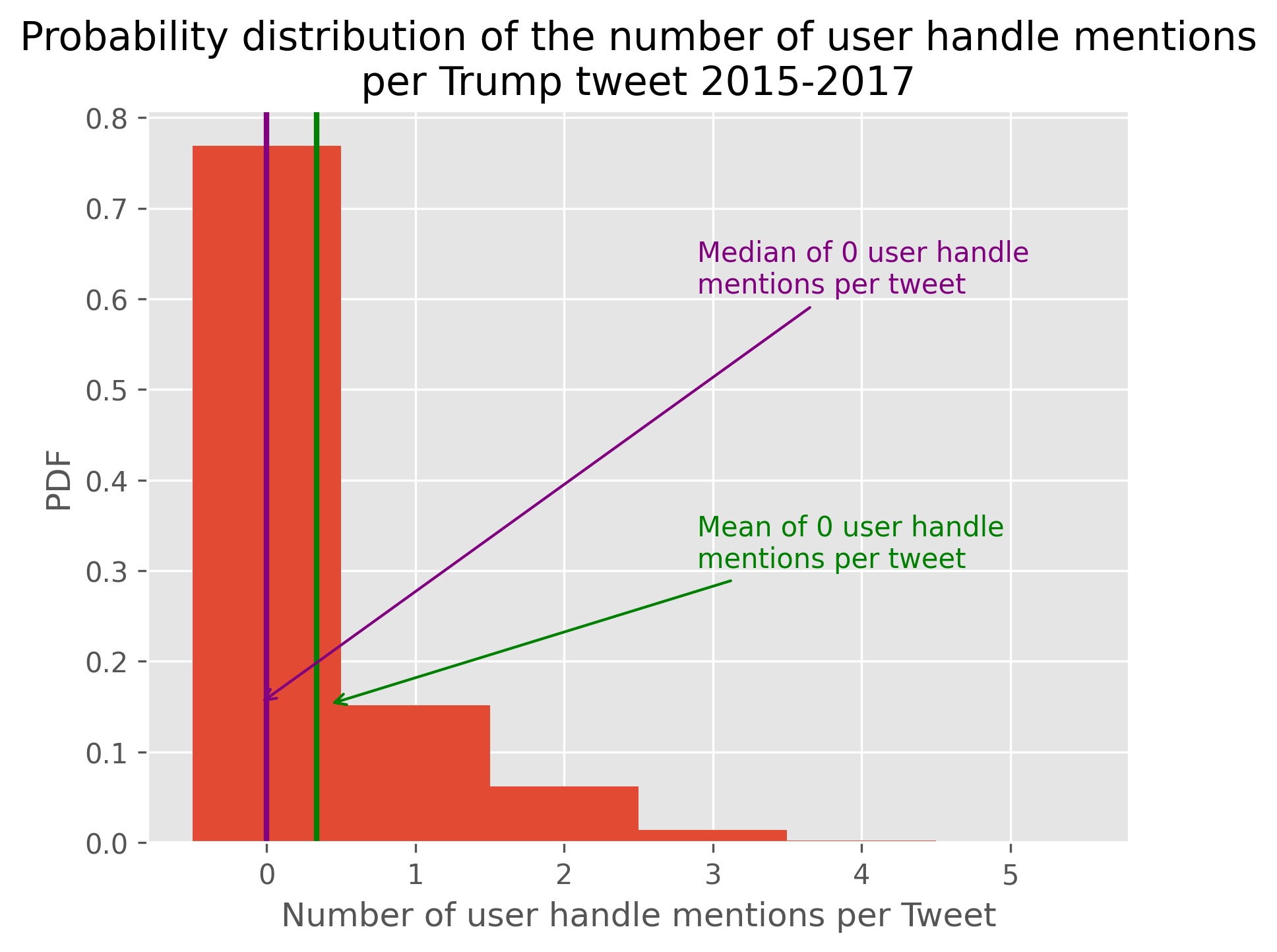
We next use Regex statements to create two more variables. The first counts the number of hashtags per tweet. Hashtags are often utilized in social media to raise attention to certain subjects, and users’ tweets can be reverse searched by which hashtags are mentioned. If a user includes a high number of hashtags in their tweet this may indicate their wish for others to recognize their perspective regarding the hashtag subject and imply some sort of call to action around the subject. The second variable counts the number of user handle mentions for similar reasons. In addition, mentioning other users directly can be a form of confrontation, which may imply more personal volatility (as in the colloquial: “don’t @ me, bro”).
Natural Language Preprocessing:
All of this cleaning will be applied to the text contained in the ‘text’ column. First we change all contractions to their base for (i.e. “can’t” becomes “can not”. This prevents our tokenizer from splitting words and removing their context (i.e. “can’t” becomes “can” , “‘“, and “t”, yielding “can” instead of it’s negation).
Next we tokenize our words. Doing this to unconventional text like tweets would normally be a nightmare, but luckily the creators of the nltk package have built a TweetTokenizer that takes into account things like hashtags and user handles as well as emojis. When we tokenize a word we take one string that contains all of our tweet text and return a list of strings containing the individual words for this tweet.
After this we convert all of our words into lowercase. This prevents our program from judging “Failing” and “failing” as two different words. We then remove all of our stop words (i.e. “and”, “the”, “a”) in order to remove noise from our data. We can also remove all punctuation marks at this point. Next we lemmatize our words. Lemmatizing converts all words to the singular present tense (i.e. “runs” and “ran” become “run”, “rockets” becomes “rocket”) so they are counted under a single entry. There are some misprints from this process: for example "Kansas" becomes "kansa" and "ISIS" becomes "isi".
Training and Test Data Split:
Before we continue our feature engineering, we must split our data into training and test sets. For example, we will eventually want to make a column for each unique word in a tweet. If we deploy this model in the future we would not be able to create a column for new data for any unique word not previously used in to create the model. By the same logic we should only engineer non-universal columns for our model using our training data. The same holds true for our variables created from unsupervised learning.
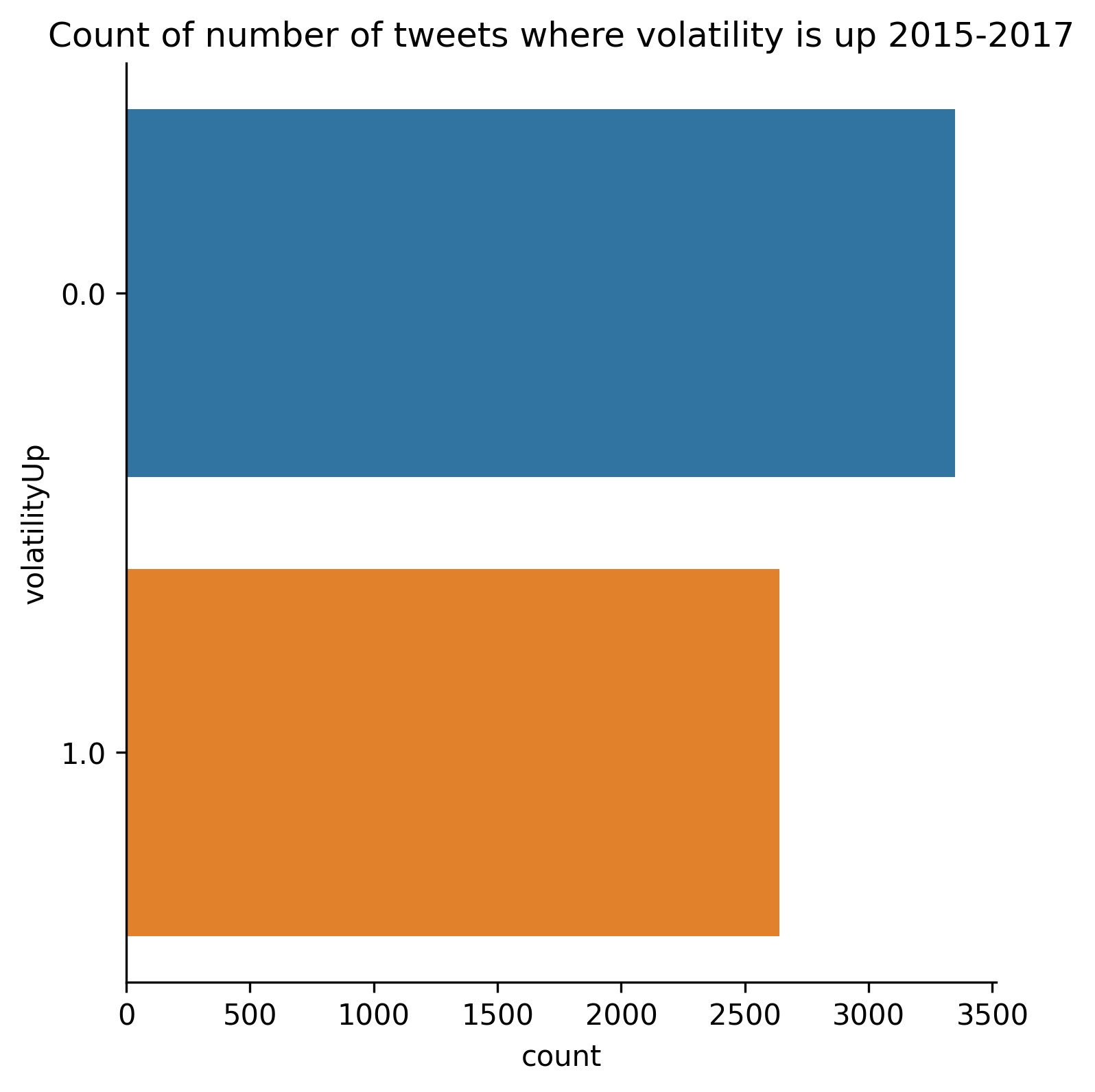
First we create our X and Y data sets holding our independent and dependent variables respectively. In this case our dependent variable is ‘volatilityUp’, and our independent variables are the data we are using to predict market volatility. We randomly sample 70% of our data for training and save the remaining 30% for testing our models. We choose to perform stratified random sampling based on our ‘volatilityUp’ variable so that we have equal proportions in both the test and training sets. This is not only because of the size of the skew between volatility entries, but the inherent nature of this skew due to volatility’s constant depreciation as discussed previously. The remaining feature engineering is derived solely from the training data.
NLP for Feature Engineering:
We created a new DataFrame containing a count of all the unique words in all of our tweets. We refine this DataFrame to the 2,500 most commonly used words of the 8,270 words used in all of the tweets. We then create a new column in our original DataFrame for each of the 2,500 most commonly used unique words and in that column count the number of times that word occurs for each individual tweet. Next we drop our lemmatized tokens column as well as our original text as they are no longer needed.
This approach most closely resembles a bag-of-words NLP strategy. On the other hand, tf-idf (term frequency - inverse document frequency) uses the inverse log to punish the counts of words within a single document if they also commonly appear in all documents. The general idea is that a word carries less sentiment the more often it is used. Tweets are highly temporal, and to me this does not account for this. Let’s say we have an extreme hypothetical scenario where a Twitter user who is running for political office threatens to imprison their political opponent upon election to office (unrealistic, I know). They may say this many times, and the words used to indicate this sentiment may eventually be used so many times that the audience becomes desensitized to them. However, due to the high frequency of tweet generation, I personally hold that it doesn’t matter as much how many times the words were used as how many times the words have been used so far. If this candidate mentions locking up their opponent the first few times, the public may react with shock, it may be in the news, and the market may react. After you cry wolf a few times, is the public going to react the same? Probably not. To me this indicates more of a need for Bayesian inference for penalizing our word counts (as in increasing the count penalty for a word the more it has appeared so far). I do not know if this approach is established and it goes a bit beyond the scope of this project so I decided to use a straight word count instead.
At this point our training data contains 4191 observations (tweets) and 2512 columns (not including the datetime index), consuming a little over 80.3 MB of memory.
Unsupervised Cluster Analysis for Feature Engineering:
Next we used unsupervised K-means clustering to create new variables.This analysis uses Euclidean distances between variables to find a mean distance between measurements and group data into clusters based on the desired number (k) of clusters based on centroid points of these distances. This allows us to group our observations as relative to one another as opposed to the dependent variable.
We use a silhouette score to gauge the appropriate number of clusters to set. The silhouette score measures the distance of observations from all clusters other than the one to which they are designated. A score closer to 1 indicates a larger distance between our clusters, meaning we have more well defined clusters. A score closer to zero indicates undefined clusters. Scores closer to -1 indicate that observations have been selected for the wrong clusters. We then iterate through between 2 and 10 clusters and check our silhouette scores.
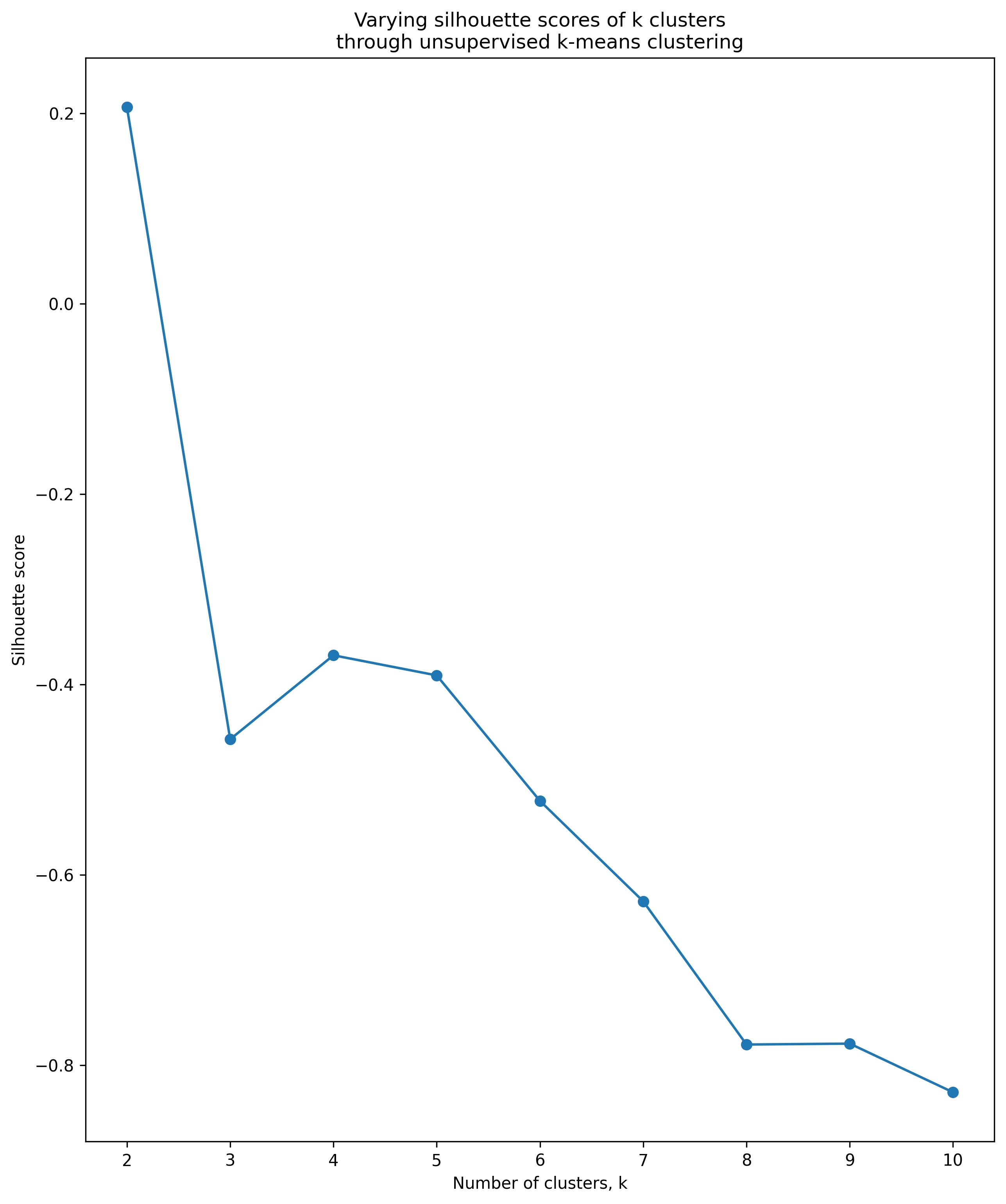
We observe that our silhouette score is closest to 1 when we set 2 clusters. We fit our model for two clusters and assign the cluster designations to a new column. We then use our existing model based on our training data to predict cluster assignment on the test data and create a new column for this set. The cluster assignments are the categories as opposed to numeric data, so we transform this column in both sets to a dummy variable (only 1 as there are two categories). To predict on our model we require the same number of columns in the training and the test sets. When creating clusters we may have created columns in our training set that do not exist in our test set (this is not possible with only 2 clusters, but is in the instance where k is determined to be higher). To remedy this we check which columns are missing in our test data, and add that column filled with a zero value if that is the case.
Our data is now starting to get pretty large. In order to save memory we downcast all of our int64s to int8s and our float64s to float32s. This reduces the memory of our training data to around 10.1 MB.
Exploratory Data Analysis:
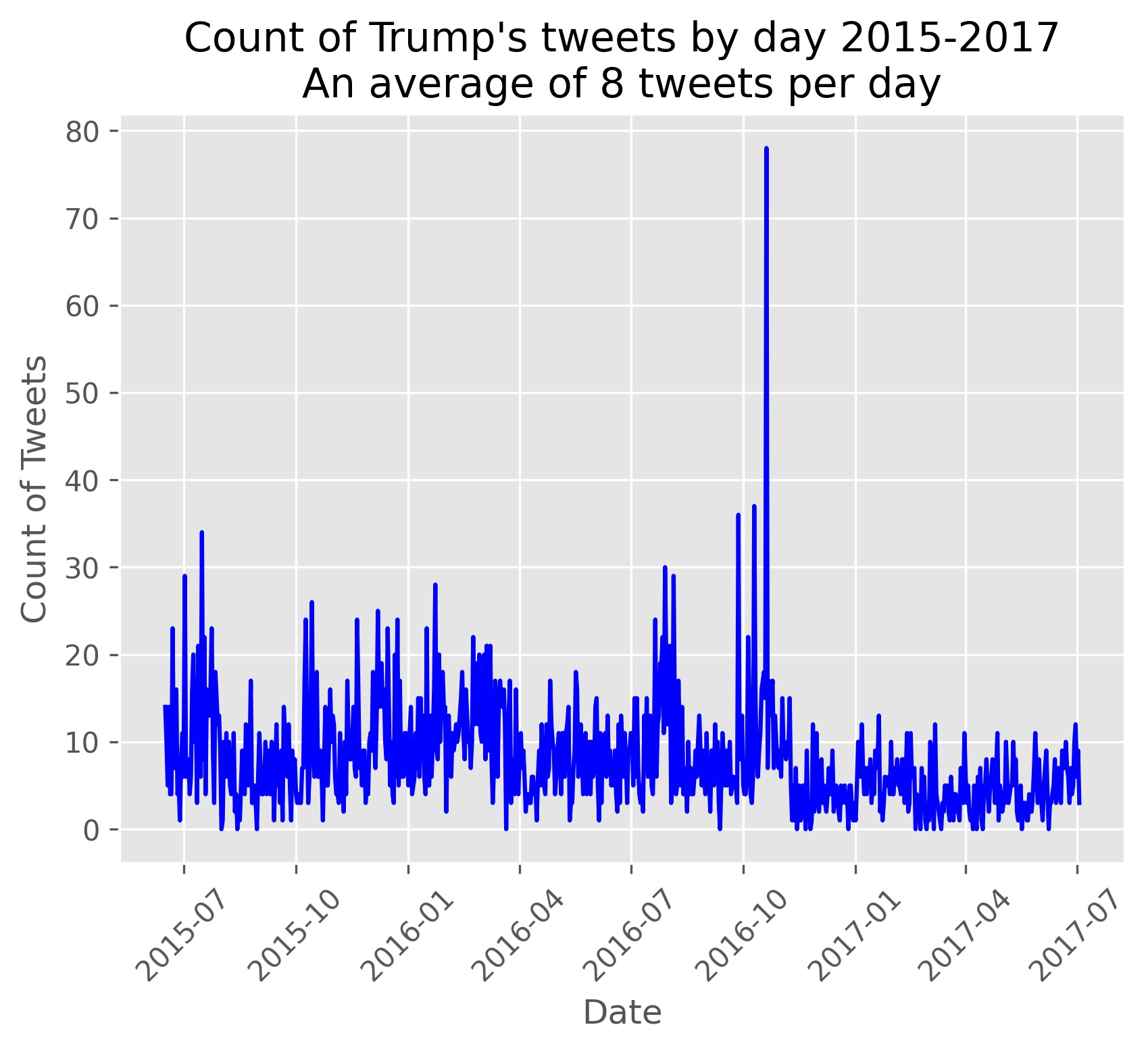
To start off I want to answer some of my most pressing personal questions. The first to come to mind is: How often is Trump tweeting per day? We resample all of our data to a daily frequency and count our observations per day. Most days range between 3 and 20 tweets with a spike near his candidacy announcement and his largest spike with around 80 tweets in a day falling around the proceeding election day.
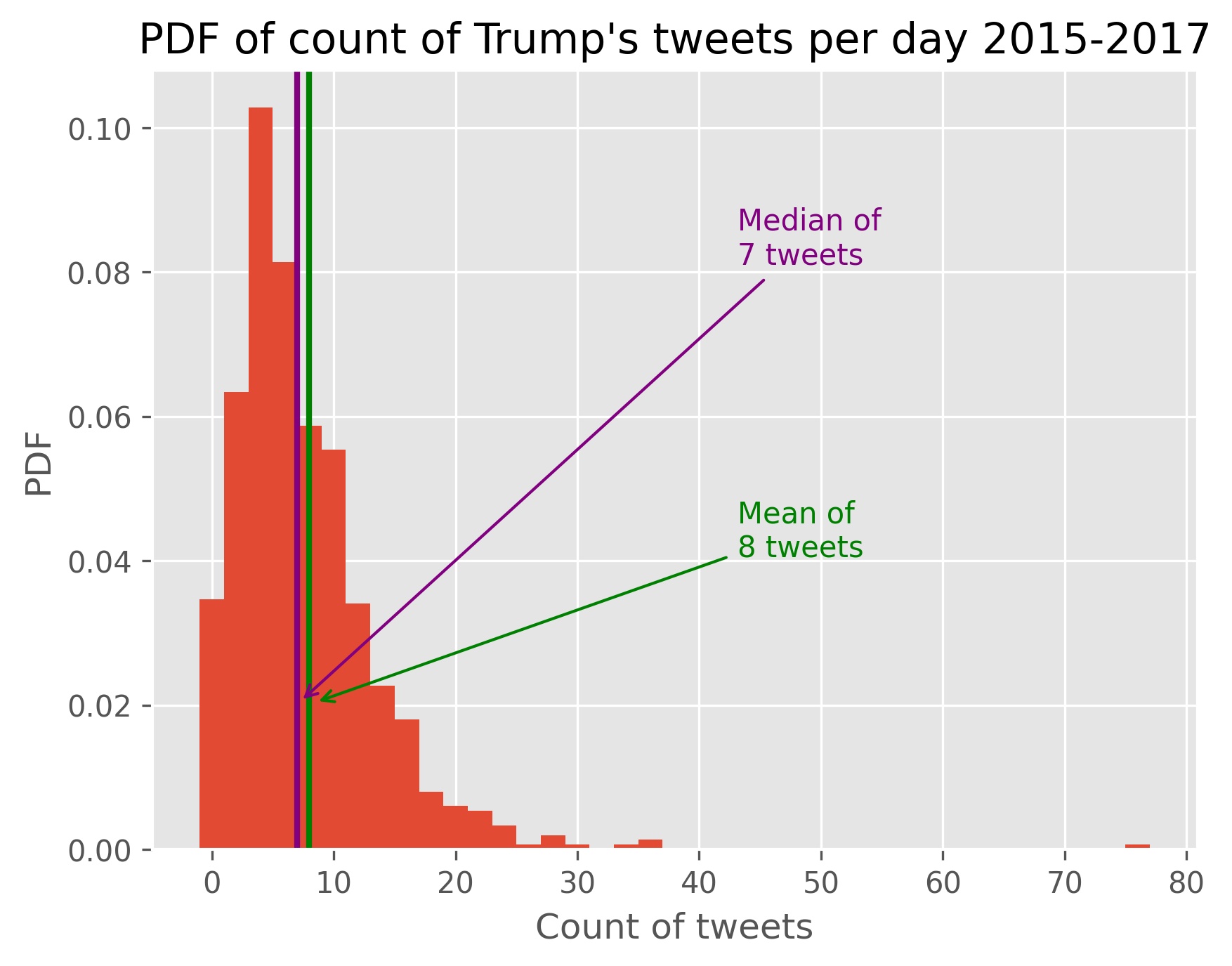
Looking at a probability distribution function of tweets per day shows a relatively lognormal distribution with a few extreme outliers.
We also want to know what time of day Trump normally tweets at. He is often depicted as tweeting late into the night. If this is the case we might expect the market to have more time to react then correct before the next open. We push our data back 8 hours to go back to calendar time from market time, resample data to 60 minutes, then create a probability distribution function to see what percent of the time tweets for each hour.
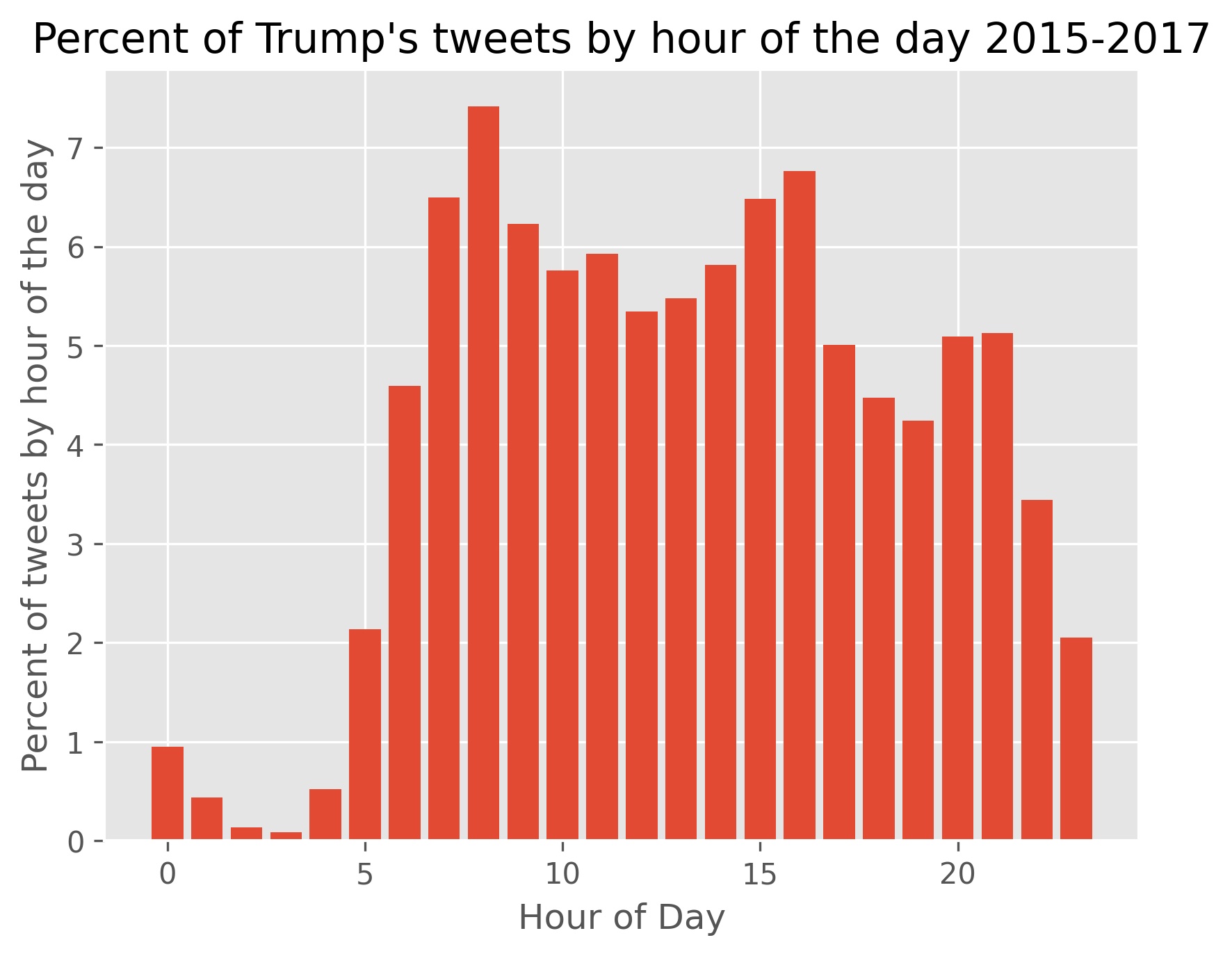
It seems that public perception of him may be a bit skewed in this case. Not too high of a percent of tweets occur past 11 PM, but there are noteworthy outliers at late hours. His activity seems instead to peak at 8 AM, with a second peak at 4 PM and a third from 8 to 11 PM. It is worth noting that this third peak occurs while FOX News airs Tucker Carlson Tonight, Hannity, and The Ingraham Angle. The president often calls in to these shows and maintains a dialogue with these television personalities via Twitter.
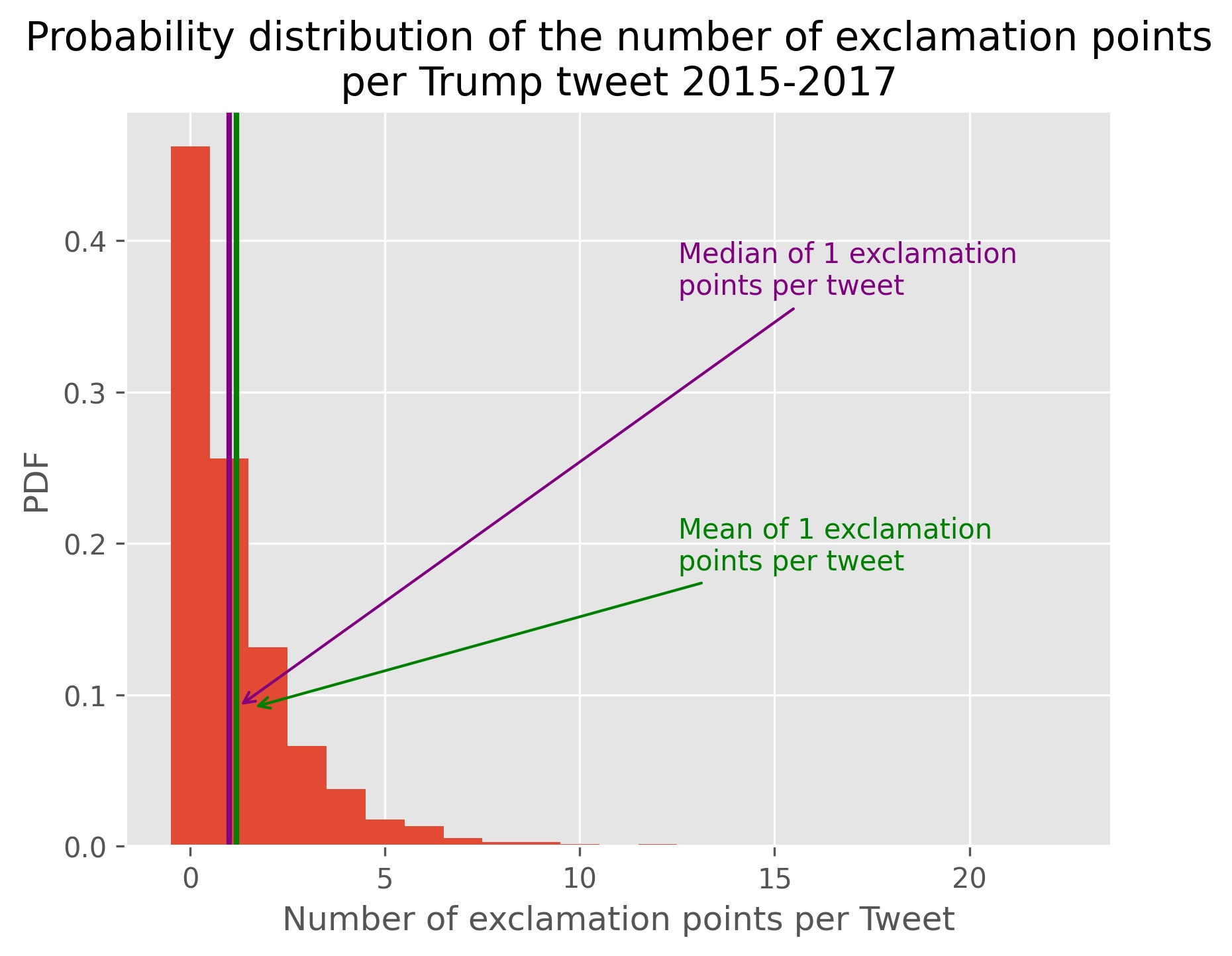
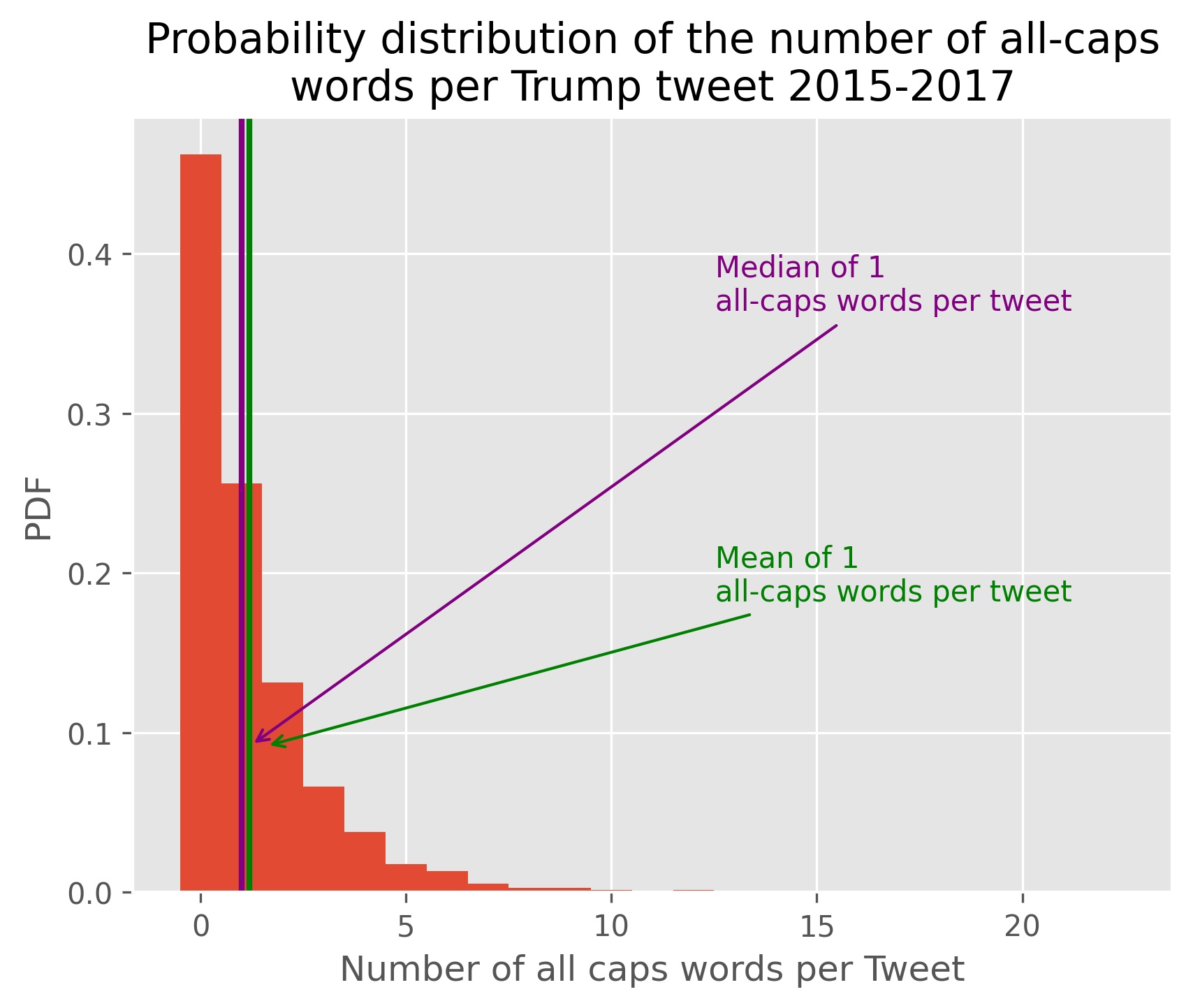
We also make histograms of probability distribution functions from the regex variables we created. These all seem to exhibit a lognormal distribution.

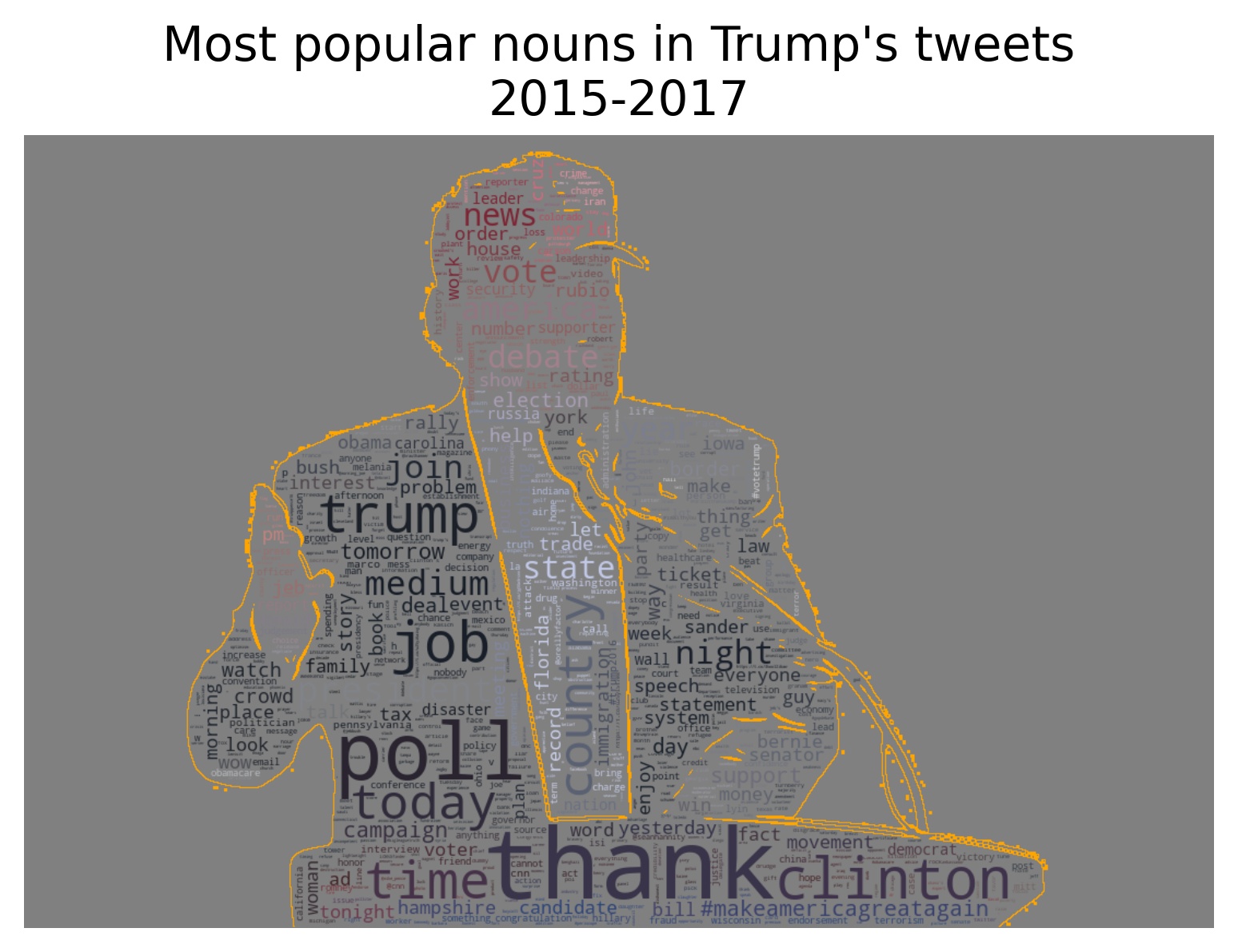
Next we want to examine our word frequency within all of our tweets. Because of the large number of unique words, a bar chart would be prohibitive beyond the top few words. We instead create a word cloud with the size of the word dependent on the count of that word’s occurrence. Oh yeah, they’re also shaped like Trump’s head. A word cloud of the top 2500 commonly used words is generated using a free image (https://www.freeimg.net/photo/868386/trump-donaldtrump-president-usa).

The title image was created by taking the 2500 most popular nouns and another free image (https://commons.wikimedia.org/wiki/File:Donald_Trump_by_Gage_Skidmore_5.jpg). Tutorials for how to fit a wordcloud to an image can be found here.
Working with Dask and memory requirements:
Although we previously reduced the memory needed for our DataFrame to 10.1 MB, we will be performing some more memory intensive model fitting and hyperparameter tuning that will make this add up quickly. Dask allows us to preserve memory in two ways. Using Dask data structures like arrays and DataFrames allows us to partition our data between our CPU cores. In this case we create 2 workers for each core, giving us eight partitions in total. Secondly, Dask allows us to parallelize our processes. Once data is stored in a Dask data structure any processes performed on the structure until it reaches a point where it is instructed to calculate (in our case the calculation is our model fit using ParallelPostFit functions). Dask then takes all the processes that are required up until the calculation and optimizes them by running processes in parallel among our workers where possible. This in turn saves us in memory usage and time required to run our program.
A natural question that may arise is why we chose this point to parallelize our data structures instead of just doing it from the start and avoiding Pandas altogether. Parallelization can save memory when implemented correctly on large amounts of data. On modest sized data the time consumed partitioning the data and parallelizing processes will actually make Dask slower than serial operations. Relatively speaking, the size of our data isn’t all that large until we engineer a column for the top 2,500 unique words in all of our text. After we do this we have greatly increased our number of data points, and I felt like this was an appropriate point to implement parallelization.
One would probably consider implementing parallelization from the beginning if this model were to be scaled up for deployment. In this case we would probably have the funding to use a higher tier Twitter API to access every tweet up to the present instead of the hard files of limited data that we are using in this project. Handling large amounts of unstructured JSON data at that scale would also be much easier in a Dask bag than treating it as nested dictionaries in a Pandas DataFrame as we have done in this project.
To parallelize our data structures we simply convert all of our Pandas DataFrames (both the dependent and independent training and test sets) into Dask DataFrames. We then convert these Dask DataFrames to Dask Arrays, which work similarly to NumPy arrays and further reduce memory requirements when model fitting.
There is one more trick we have up our sleeve to save memory and time. Our array has 2,500 columns that contain counts of unique words. Considering a tweet only has space for 250 characters and we aren’t counting common filler words like participles, that leaves us with a very large amount of data points that contain the value zero for the times a word is not mentioned in a tweet. This type of data is known as ‘sparse’ (as opposed to ‘dense’). Our value of zero is still a value and matters for our models, but in terms of memory this is a lot of redundant information and takes up the majority of the memory needed for our array. We take a shortcut around this by converting our Dask arrays into compressed sparse row (CSR) matrices. We know that we are going to be using matrix dot multiplication in our models, and that the product of anything and zero is equal to zero. Therefore, we are wasting a lot of memory when we make a model calculate a data point where we already know the answer. Instead of using the memory to hold a value of zero, we essentially fill in a NA value anywhere there is a zero in the original array. Then we tell our array that any calculation performed on that point will yield a zero. This saves us memory and time (and keeps the program from crashing!). We have done this after converting over to Dask, so these data structure conversions are delayed as well.
Dimension Reduction with Truncated Singular Value Decomposition:
We have a very large number of columns so far, but not all of them are necessarily relevant on their own in regards to what we want to predict. We can use singular value decomposition to discover concepts within our data and reduce our input data to our models down to the core concepts inferred by single words. Normally we would accomplish this by performing Principal Component Analysis (PCA), which is essentially truncated singular value decomposition performed on centered data. While we are normalizing our data by scaling before feeding it into our dimension reduction and any models that we will use, if we were to standardize our data with a mean of zero our sparse matrix would suddenly become dense and consequently take up much more memory. We can simply perform truncated singular value decomposition on our scaled data to preserve the sparsity of our matrix. As we want the same size array going into each model, we will be applying the same hyperparameter setting for the truncated singular value decomposition to every model that we will be fitting from here on.
We choose the optimal number of dimensions, or concepts, to decompose our data down to based on the accuracy score achieved through 5-fold cross-validation on a baseline model. In the case of a classification problem we choose a logistic classifier as our baseline model. We choose the ‘saga’ algorithm to solve our logistic classification as it works a bit faster on large datasets and will allow us to use elastic-net penalization in our later models’ hyperparameter tuning. The baseline model also allows us to observe which variables are given highly weighted coefficients before performing truncated singular value decomposition. After this point our variable will be reduced to abstract concepts that will limit model interpretability, so it is helpful to get a gauge of unique words that may have a large impact on volatility.
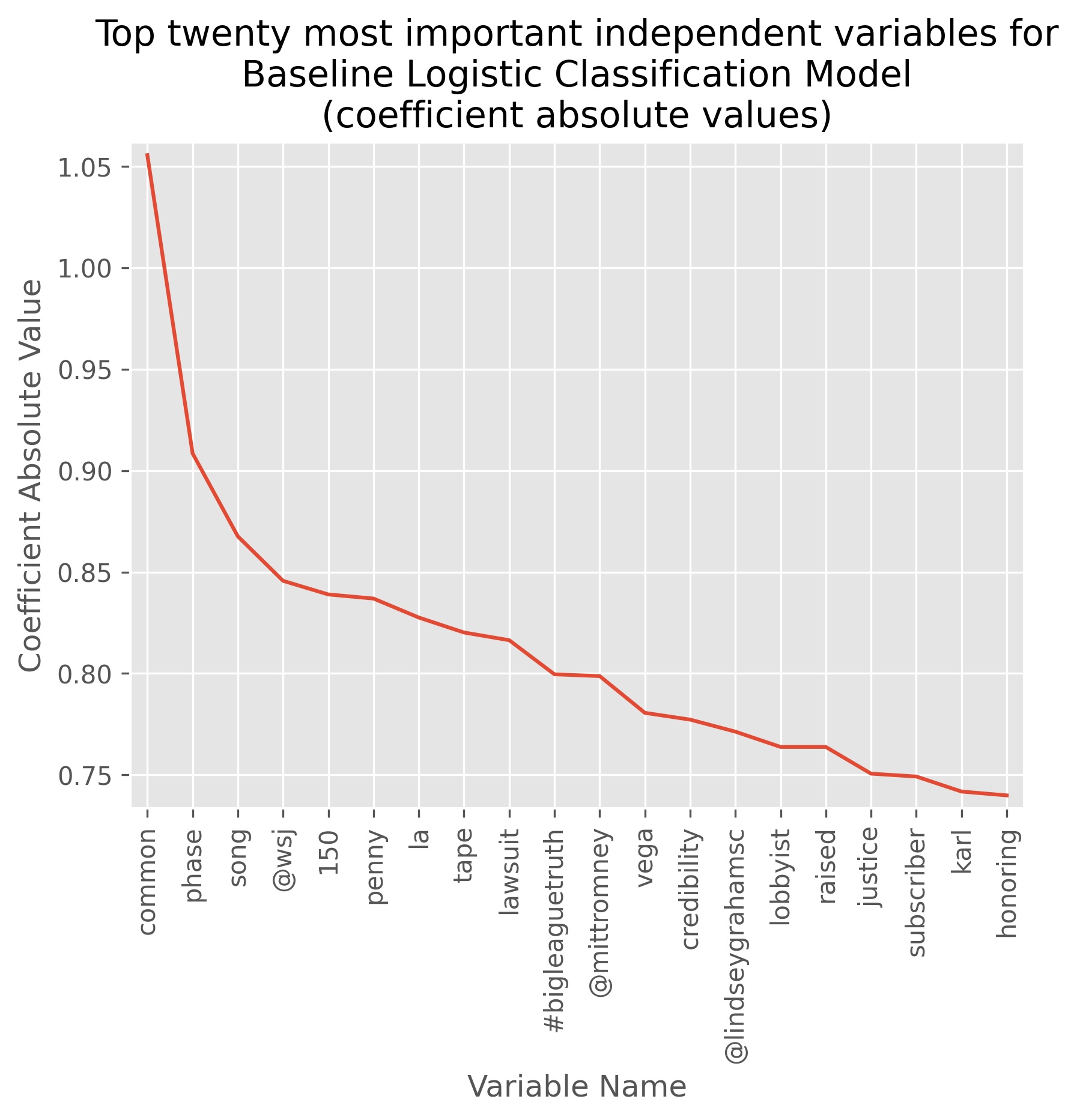
In order to visualize what unique words are given the most weighting, we take the absolute value of the coefficient weighting for each word and then sort them descending by absolute coefficient weight. The top three words (‘common’, ‘phase’, and ‘song’) don’t seem to carry any noticeable connotations, though the word ‘song’ may have some relation to controversy revolving around the national anthem at the time. Some notable words do appear in our top twenty most important variables. In fourth place is ‘@wsj’ in reference to the Twitter user handle for the Wall Street Journal, a publication that he is known to dislike. The word ‘penny’ is possibly a reference to his 2016 campaign to reduce fiscal spending known as his “Penny Plan”. The word ‘tape’ is a bit more ambiguous as it could possibly refer to either a controversial recording of him speaking disparagingly of women on a bus, or this could possibly refer to a controversy surrounding alleged acts taking place in the presidential suite at the Ritz-Carlton hotel in Moscow (both of these stories were prevalent in US news during the time of the twitter data used in this project). An ambiguous pair of words that both appear in the top twenty are ‘la’ and ‘vega’. Stemming and de-capitalizing gave us these words from either ‘Las’ and ‘Vegas’, or it could be from ‘LA’ (Los Angeles) and ‘Vegas’. There were many events this could refer to, but some notable ones were Trump saying he would like to punch a protester in the face in Las Vegas in 2016, Trump winning the Republican primaries in Nevada, remarks on a mass shooting in Las Vegas in 2017, or it may in the context of expressing general animosity towards the traditionally liberal city of Los Angeles. Two of his opponents in the 2016 Republican primaries (Mitt Romney and Lindsay Graham) are also mentioned. In this light, it is also worth noting that markets have tended to indicate higher volatility during the uncertainty of election cycles.
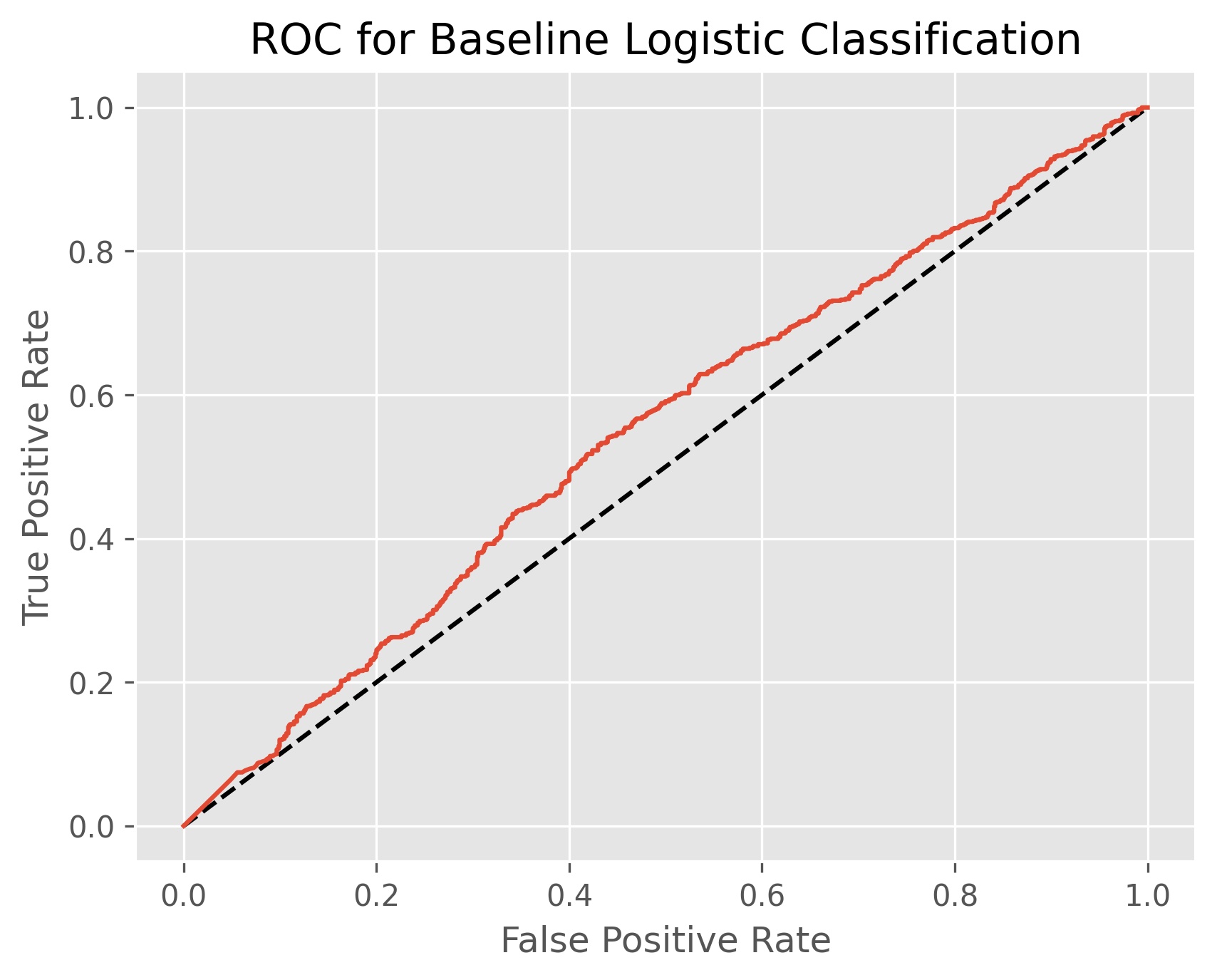
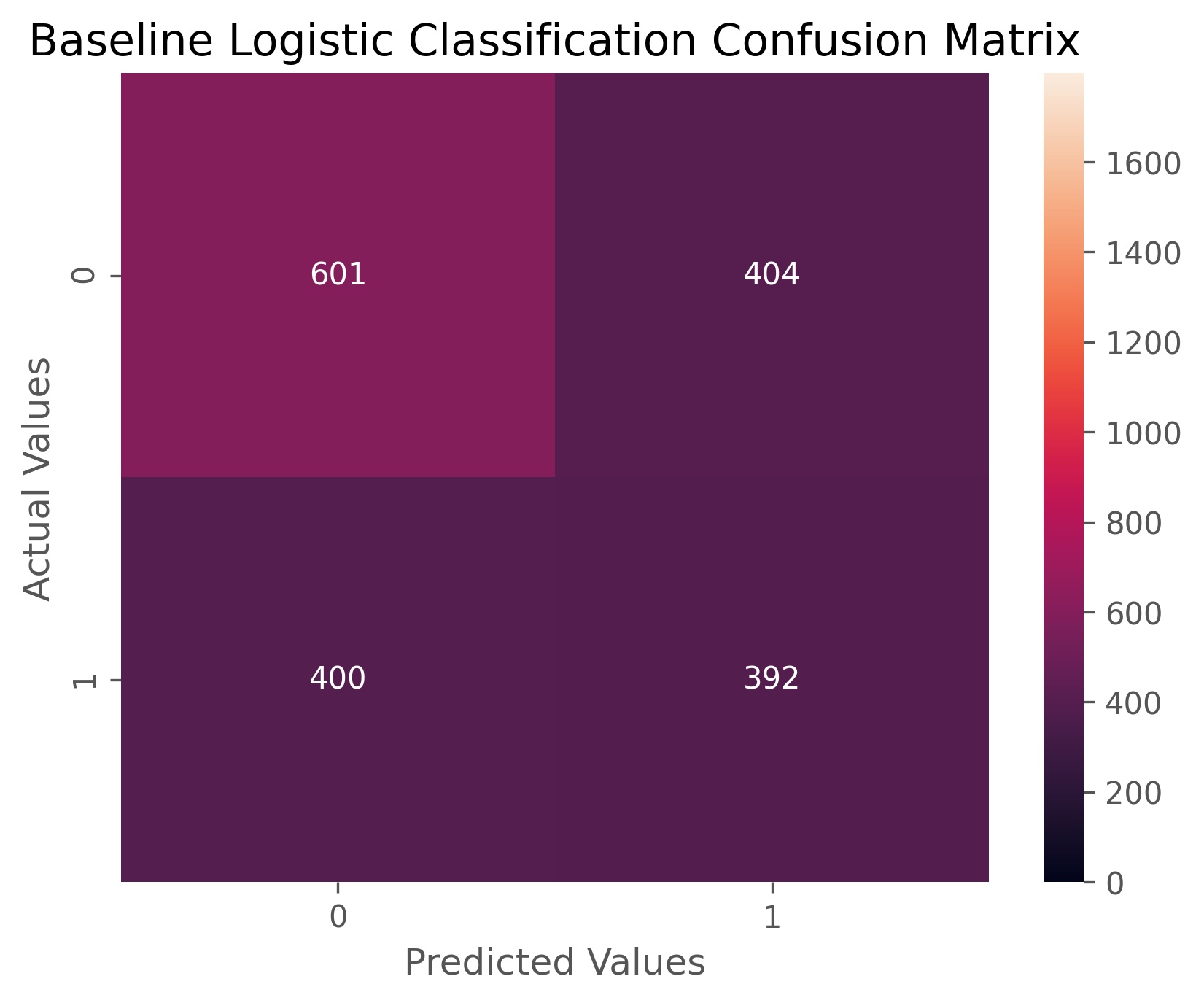
Our baseline logistic classifier achieved an accuracy score of 55.3%, and an ROC AUC score of 54.8%. In essence this means that our baseline model is only five percent better than flipping a coin, and a little worse at correctly assigning categories for each case. If we look at our confusion matrix above we can see that our baseline model is only ‘okay’ at picking out when volatility won’t happen, and when it does indicate higher volatility it is more often wrong than it is right.
The desired number of conceptual columns can vary for each problem, but it is generally recommended to use around 100 for latent semantic analysis. We use grid search cross-validation on truncated singular value decomposition we search between 80 and 120 dimensions based on the best accuracy score after being passed to the baseline logistic classifier.
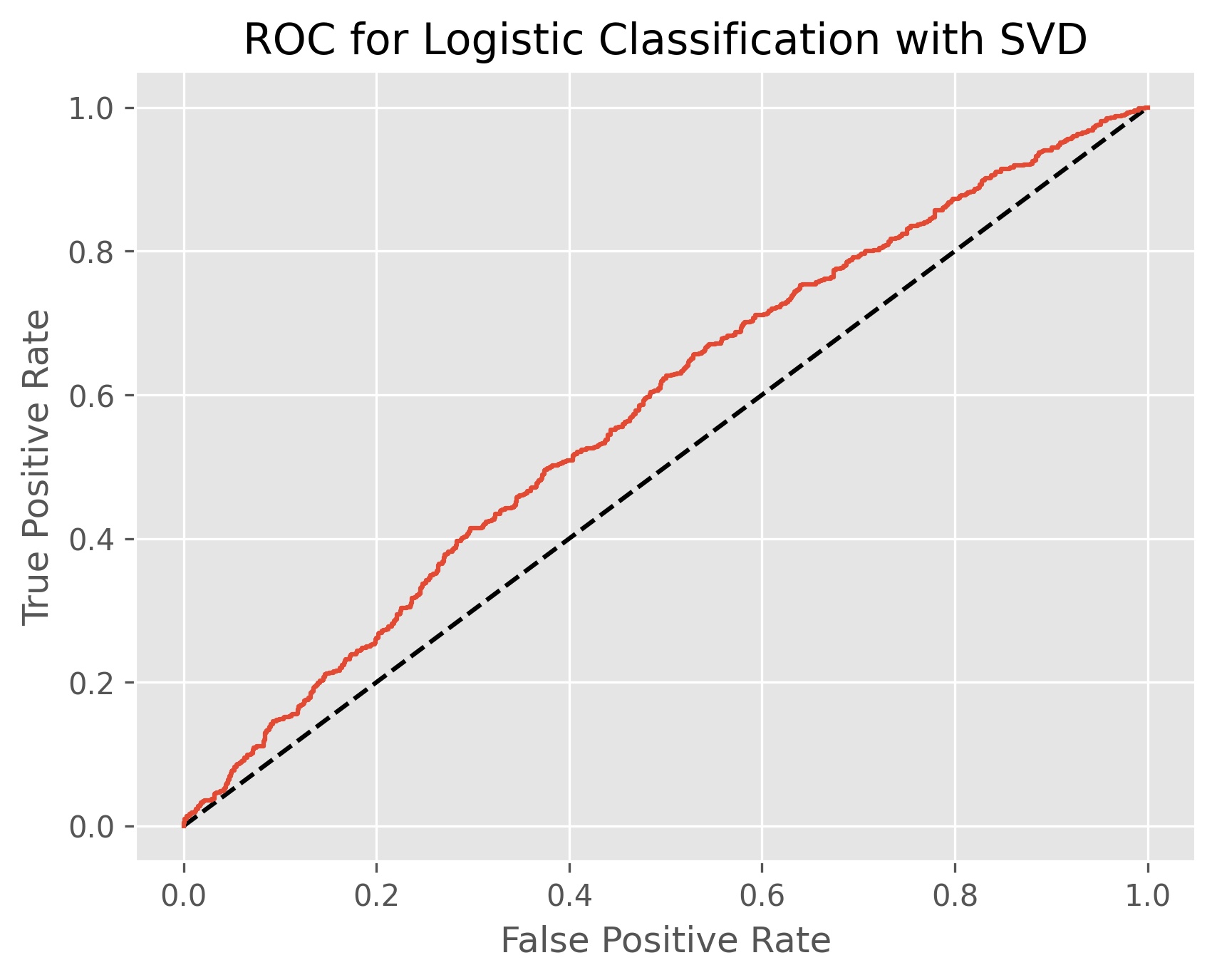
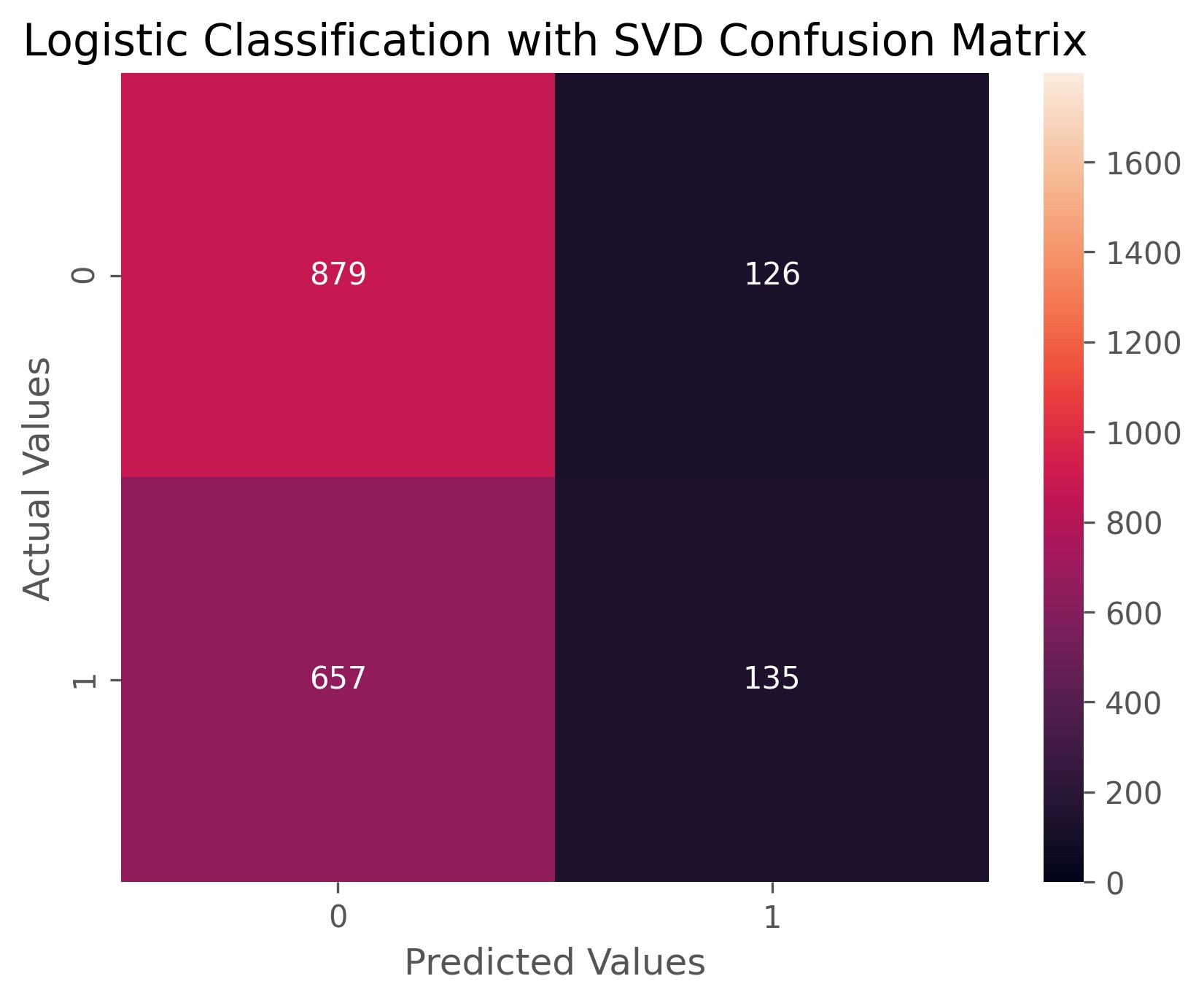
After running our cross-validation the hyperparameter of 88 desired dimensions is selected. This yields an accuracy score of 55.3% and an ROC AUC score of 57.6%. This means the model performs essentially the same as the baseline model, but it is better at correctly identifying each class. We can see from our confusion matrix that the model has significantly improved on days where volatility is down, has worsened at identifying high volatility days, and is in general predicting high volatility less often.
Tuned Logistic Regression Classifier:
Now that we have determined the optimal number of conceptual dimensions to feed into our model, we can fit a tuned logistic regression to our data. We take the same logistic regression classifier that we used in our baseline model and tune it using grid search cross-validation. We search through C (the inverse of our regularization strength) between -4 and 4. We search through our l1 penalization ratio between 0 and 1.
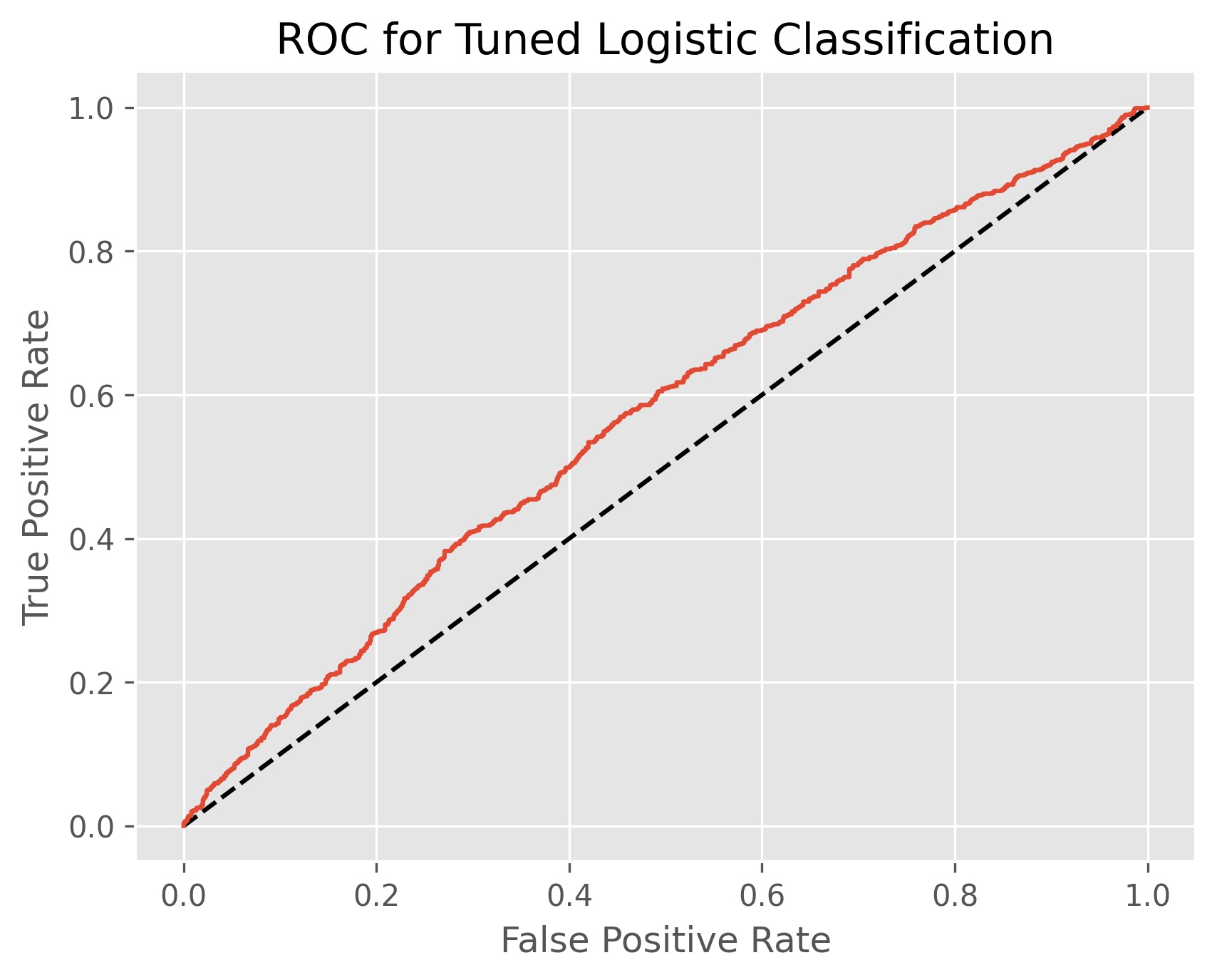
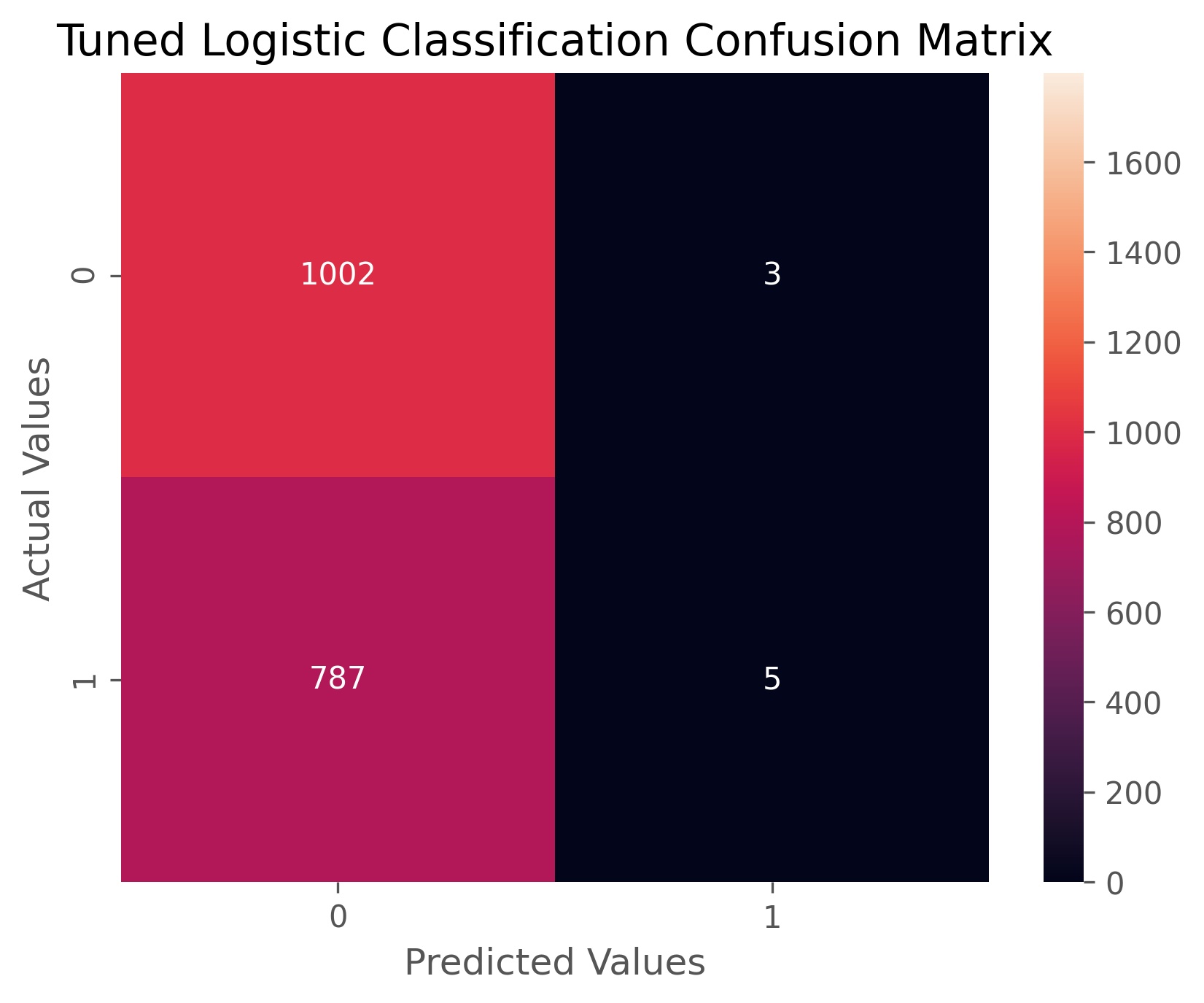
Our tuned logistic classifier search returned an optimal C value of 0.00026366508987303583 and a l1 ratio of 0.030303030303030304. The l1 ratio reveals that the model is closer to a Ridge regression than a Lasso regression, meaning that we are weakening coefficients more than we are deselecting them altogether. The tuned logistic classifier achieved an accuracy score of 56% and an AUC ROC score of 56.9%, meaning we are overall better at predicting, but our ability to correctly identify each class has decreased. If we look at the confusion matrix above, we can see that the model is predicting nearly every event as not higher volatility. It Has greatly improved its ability to do this, but at the cost of losing nearly all ability to identify when volatility will increase.
Decision Tree Classifier:
We next fit a Decision Tree to our SVD data using grid-search cross-validation on the information criterion (between ‘gini’ and ‘entropy’), the maximum tree depth (between 2 and 100), and the minimum number of samples per split (between 2 and 40).
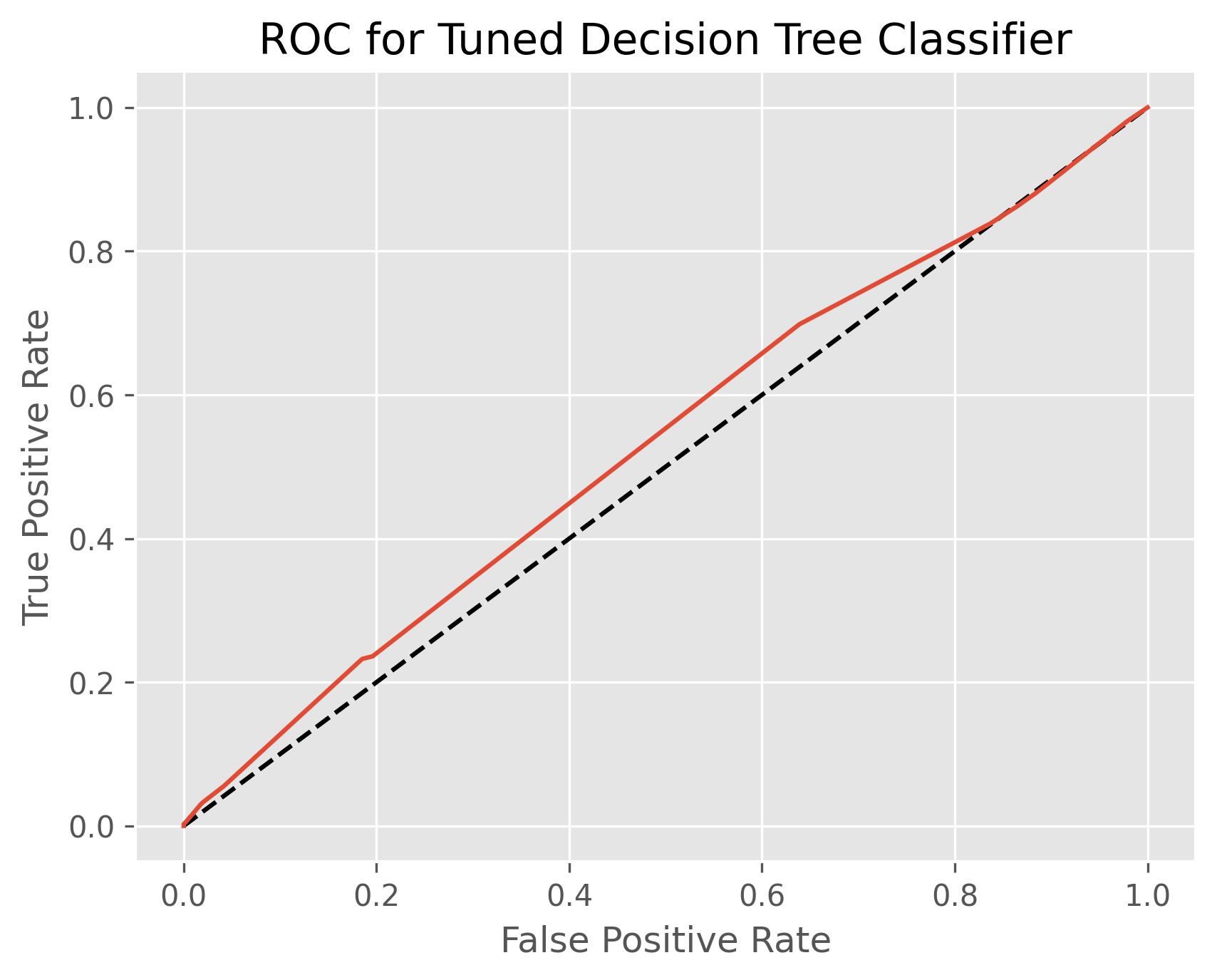
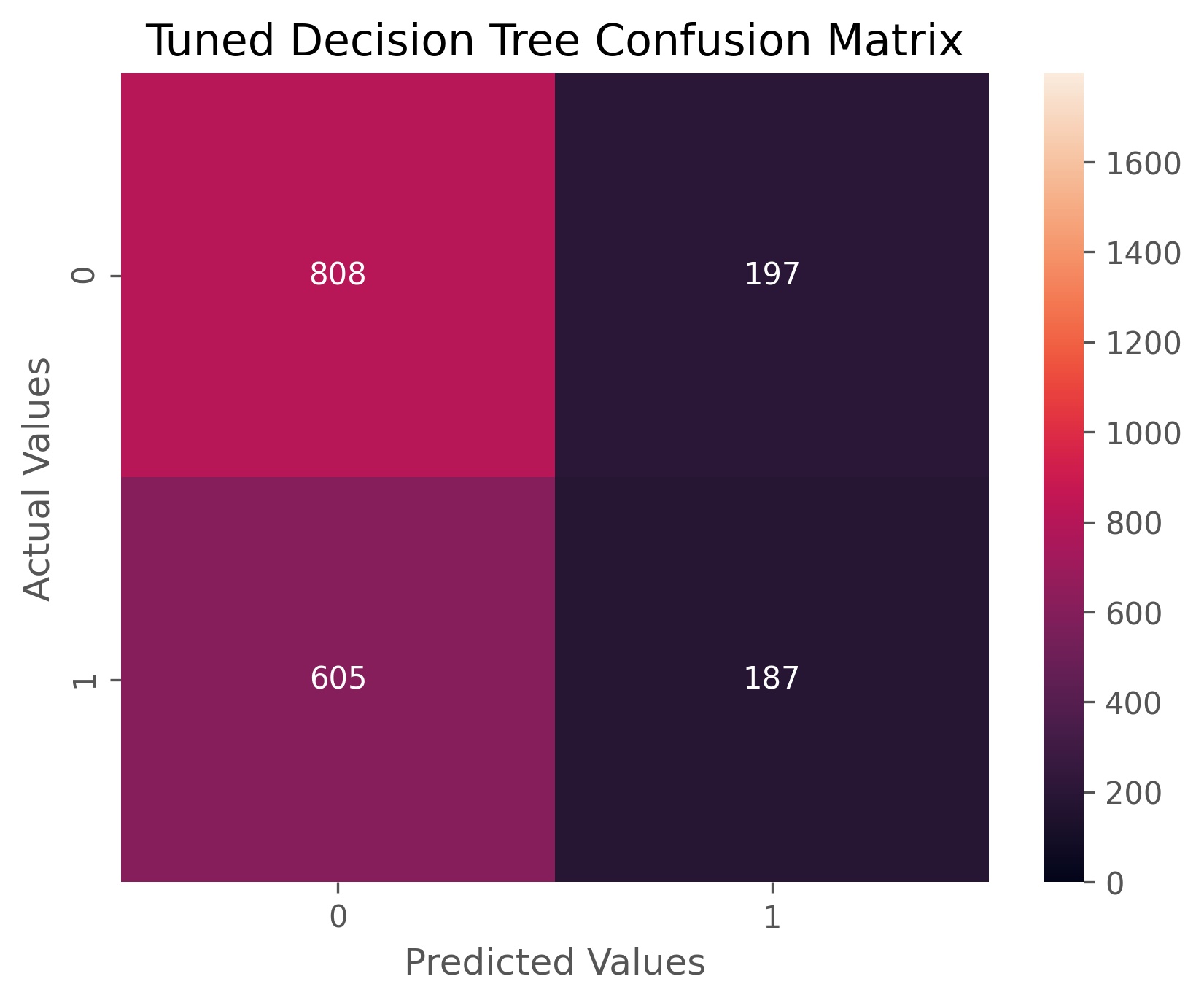
Our grid search returned a decision tree with gini information criterion, a max depth of 4, and a minimum of 36 samples per split. Our tuned decision tree achieved an accuracy score of 55.4% and an ROC AUC score of 53.3%. We can see that both our accuracy and ability to correctly identify each class is not as good as our previous models, but if we look at our confusion matrix we can see that our model is a lot less one-sided than our previous model and gives us more predictions for when volatility will be high. This lower accuracy score is to be expected for a decision tree. While decision trees are great at describing current data, they are often less able to classify new samples.
Random Forest:
We can construct a random forest of decision trees to try and make up for this inclination of decision trees to give undesirable predictions. A random forest first bootstraps our data by randomly selecting samples with replacement. We then create a decision tree for each bootstrapped data set, but only select a subset of the variables to predict on for each split. We repeat this hundreds of times, and this gives us a random forest. We then bag these results to determine our outcome by majority vote of our trees. We use grid search cross-validation on our optimal number of trees between 400 and 600, and the maximum number of features between the square root and natural log of the number of columns given by our SVD data.
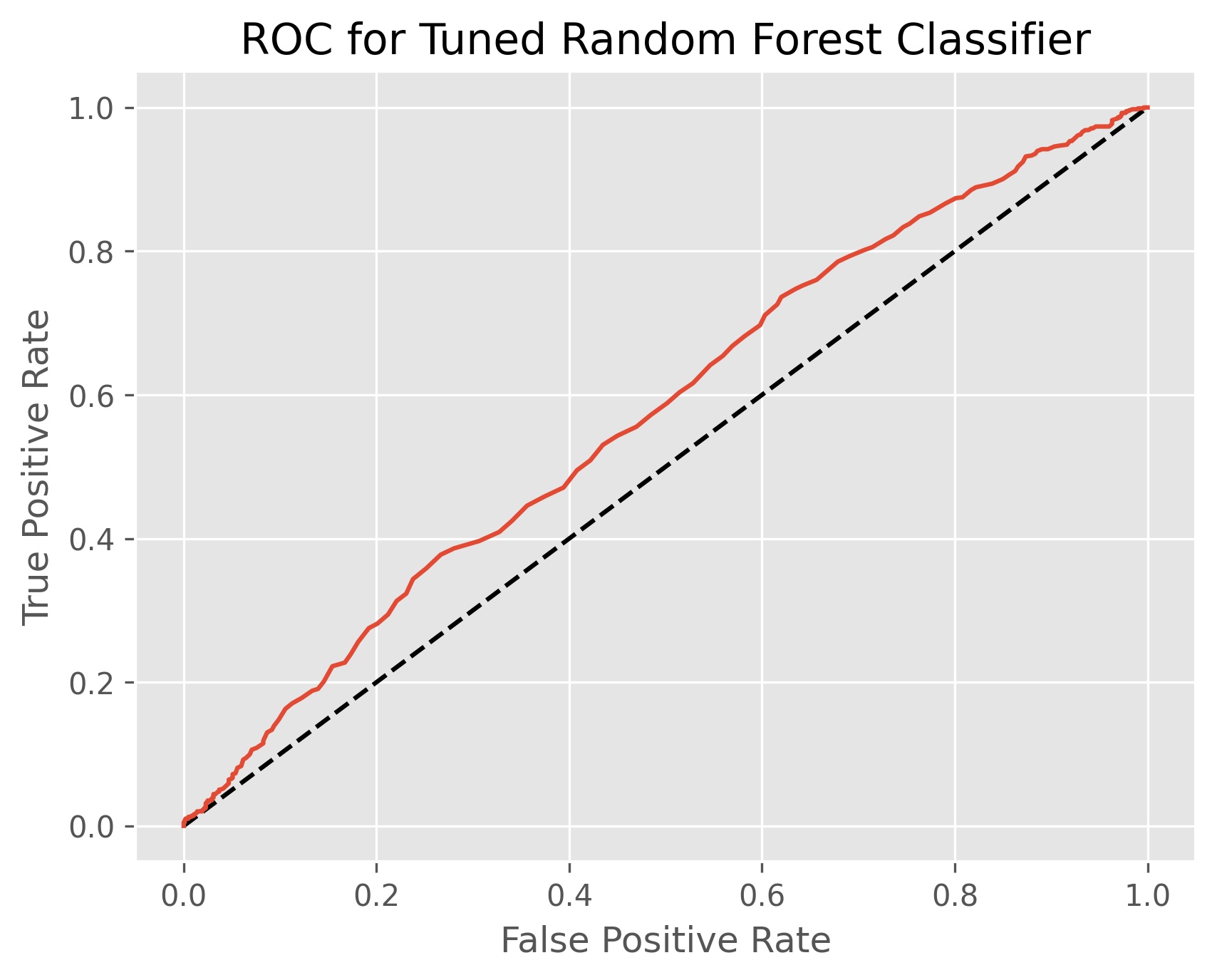
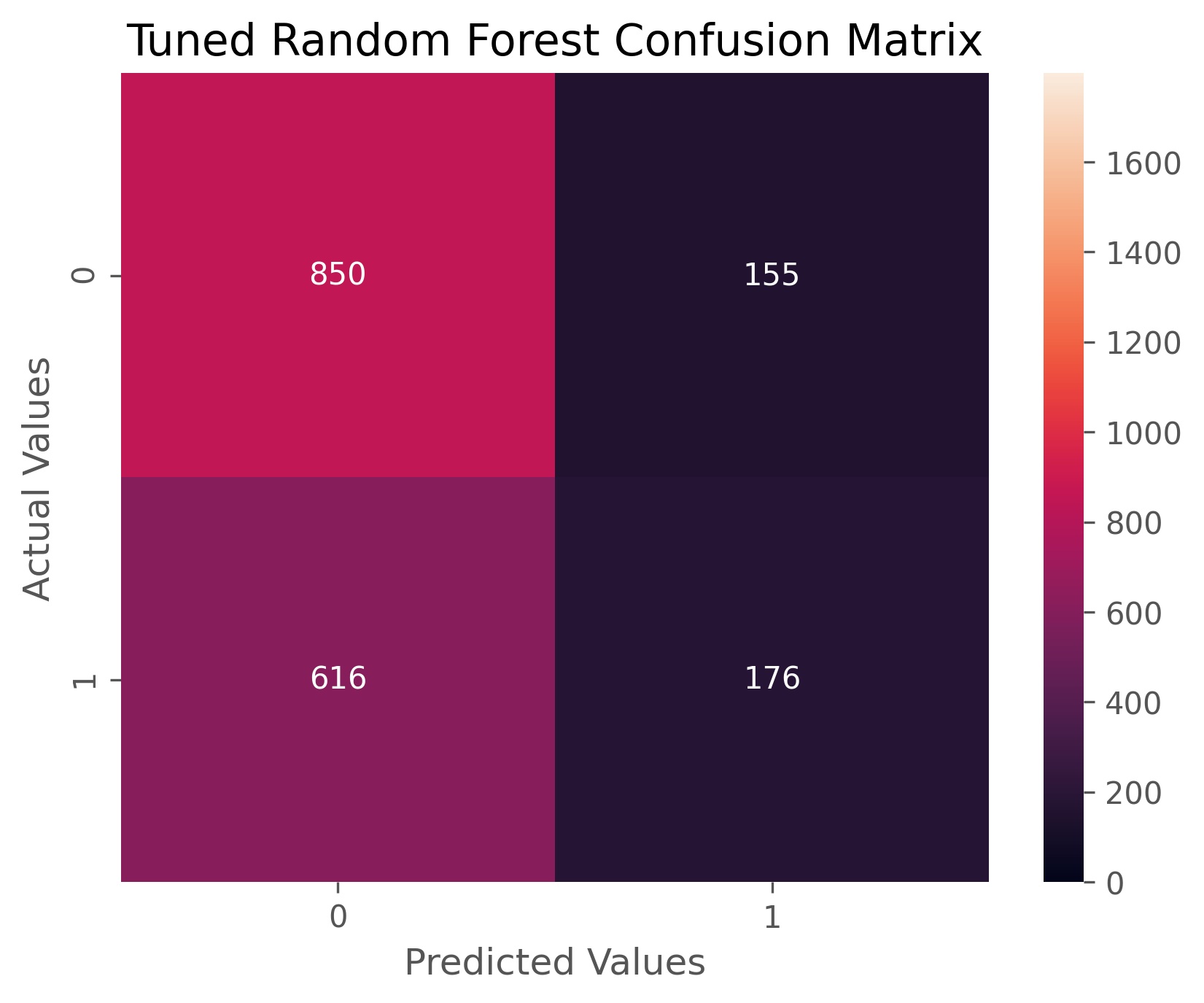
Our grid search returns the optimal number of decision tree to be 400 and the maximum number of features to be the square root of the number of columns given by the SVD data. Our random forest achieved an accuracy score of 57.1% and an ROC AUC score of 57.2%. This model is overall more accurate than the previous models, worse at predicting when volatility will be higher, and better at predicting when the volatility will not be higher.
Adaptive Boosting Decision Tree Classifier:
AdaBoost is another way we can create a forest of decision tree classifiers. In opposition to a random forest where base decision trees can be of varying depth, in Adaboost we create decision tree stumps with just two leaves. In the bagging stage of our random forest we count each vote equally, whereas in Adaboost we weigh each tree’s vote by it’s performance. We then adjust weights to each sample for each decision stump successively in order to gain our adaptive edge. We then perform grid search cross validation on the number of decision trees we will use between 50 and 1000 stumps.
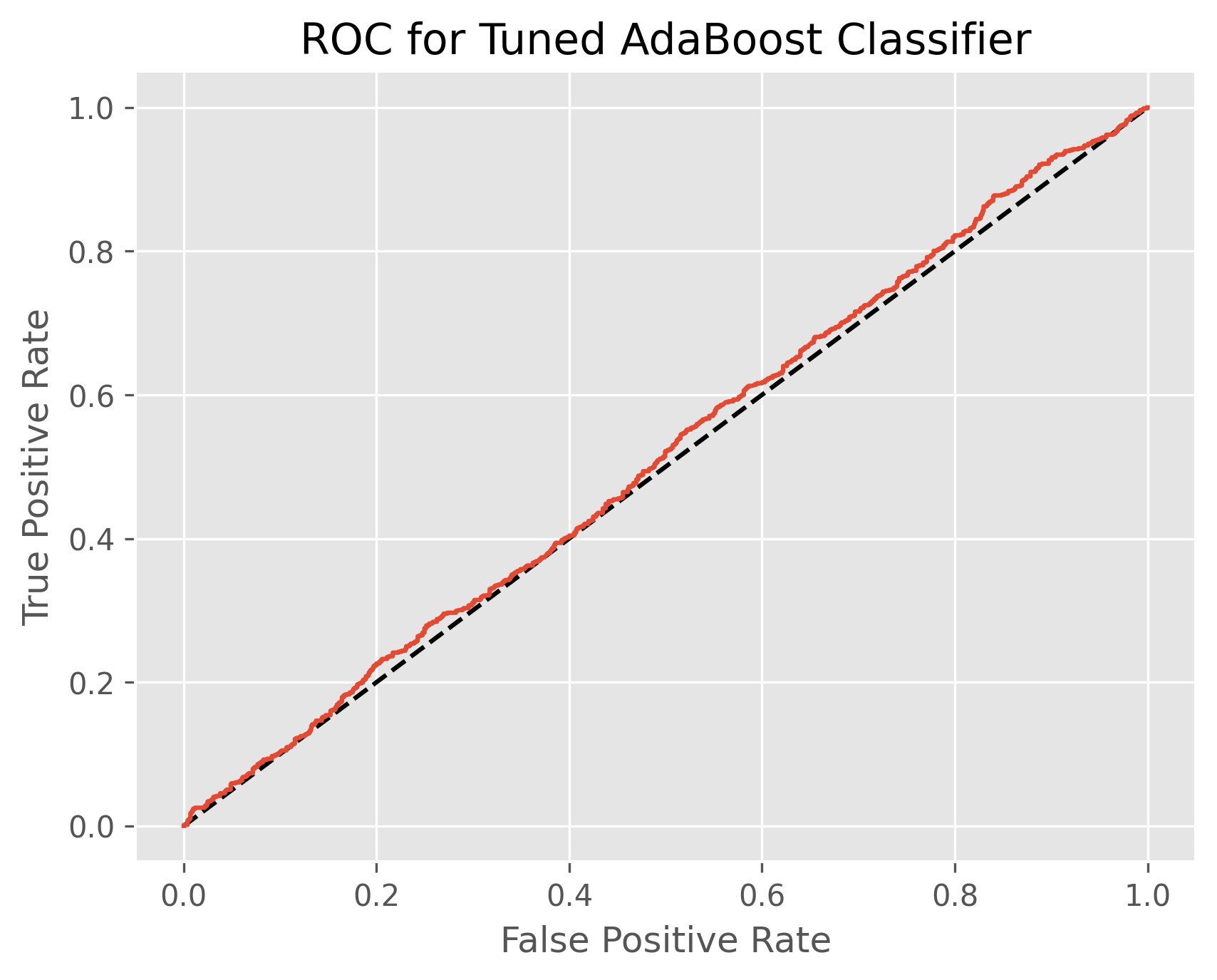
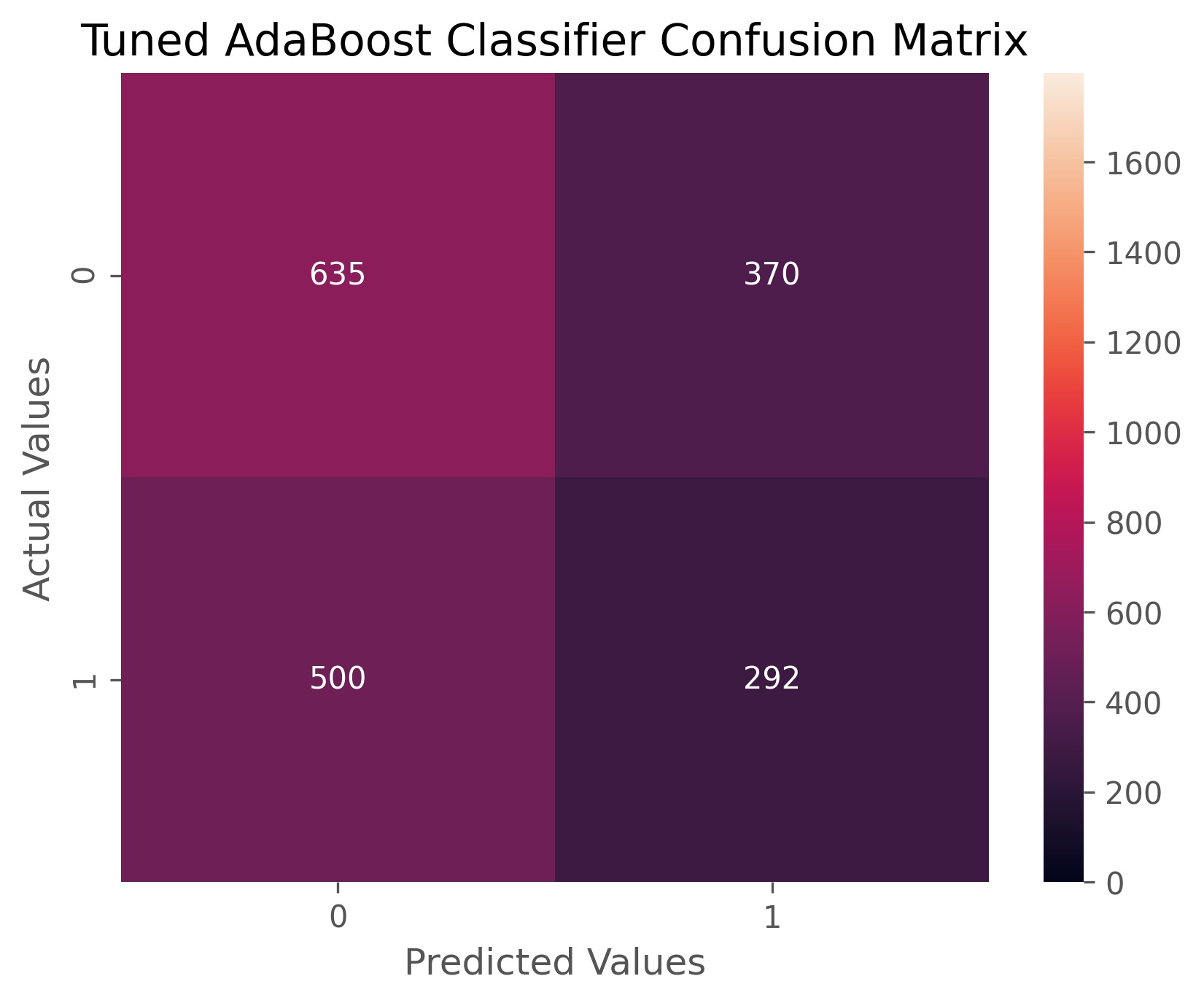
The optimal number of decision trees determined by cross-validation was 200 stumps. Our AdaBoost classifier achieved an accuracy score of 51.6% and an ROC AUC score of 51.4%. This is our worst performing model in terms of accuracy so far, but it is worth noting that this model is better at classifying when volatility goes up than our earlier models.
Stochastic Gradient Boosted Decision Tree Classifier:
In a gradient boosted decision tree classifier we build a first model, but then successively build models based on the residuals of the previous model. Our final prediction is then the sum of all the predictions of all the models. The difference between gradient boosting and stochastic gradient boosting is that each model is fitted with a different random subsample of the data in order to prevent overfitting of the ensemble results. We perform grid search cross-validation on the number of models to construct in a range from 10 to 100, and we allow our model to choose to be stochastic if it provides optimal results with a subsample size ranging from 40-100%. A selection of using 100% of the data would indicate that the model is not stochastic.
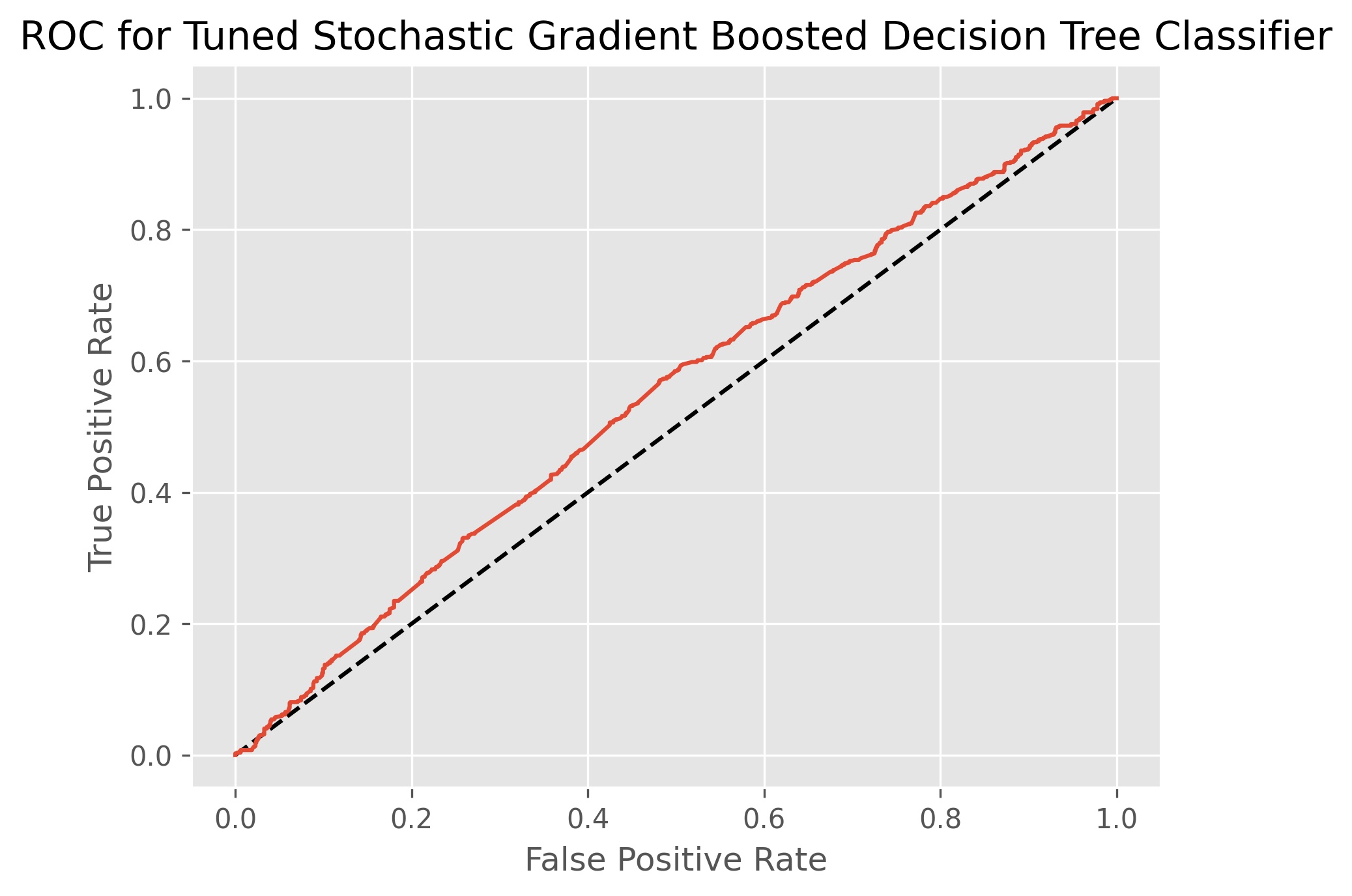
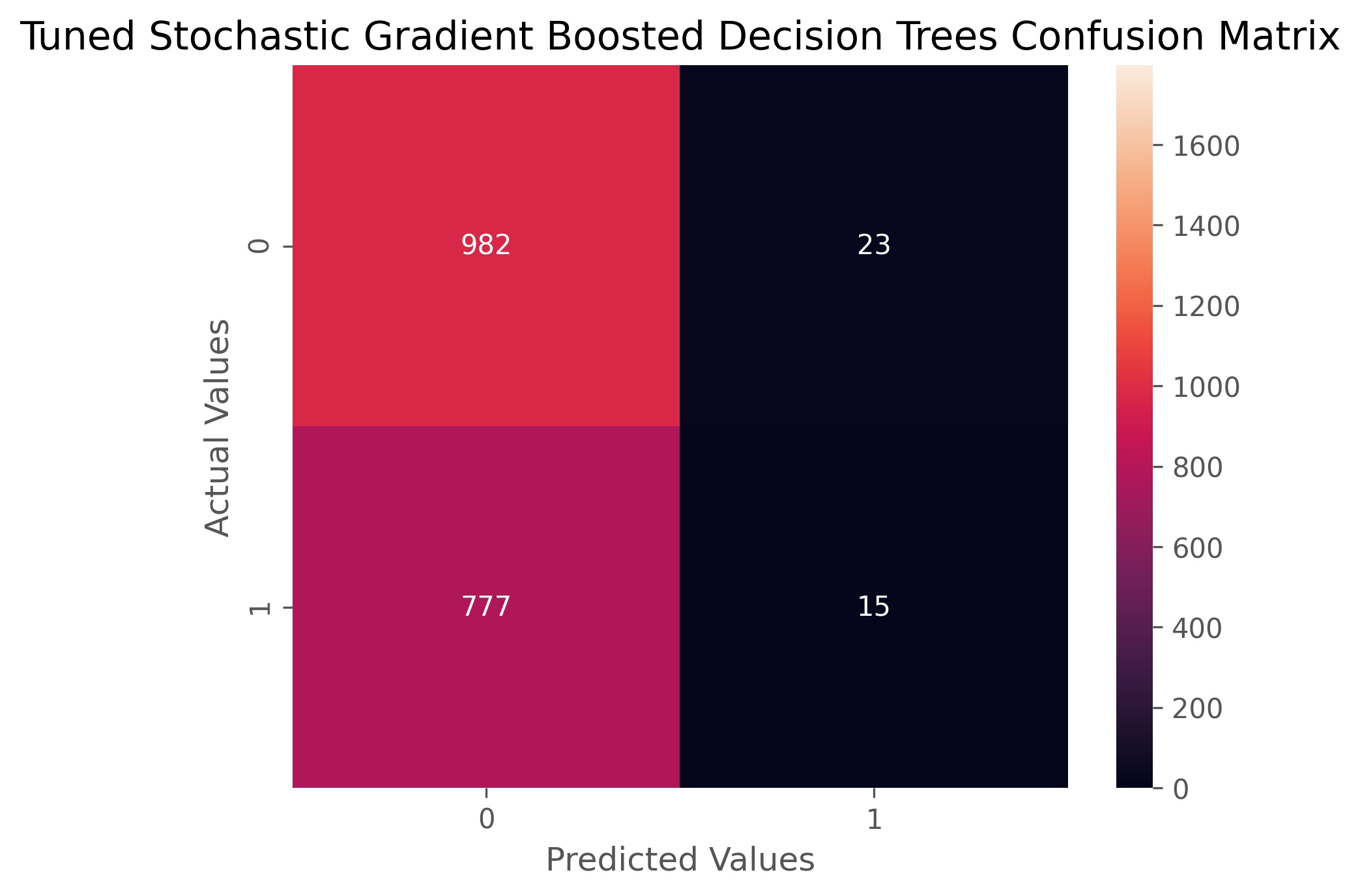
The hyperparameters selected through cross-validation are 10 models and a subsample size of 90%. This indicates that our model is stochastic. The gradient boosted decision tree classifier achieved an accuracy score of 55.5% and an ROC AUC score of 54.8%. This model is very good at indicating when volatility will not be up, but it is conversely pretty awful at correctly picking when volatility will be up.
Model Ensemble Voting Classifier:
All the models that we have made so far either don’t have too much predictive power or are only good at selecting when volatility will not be up. This variety of models may be good at identifying classes in different ways. In order to use this to our advantage, we create another meta-estimator consisting of all of our previous models, and tally the votes. We weigh each model’s vote by it’s accuracy score. The tuned logistic regression was given a voting weight of 20.3%; the decision tree at 20.1%; the random forest at 20.7%; the AdaBoosted decision trees at 18.7%; and the stochastically gradient boosted decision trees at 20.1%.
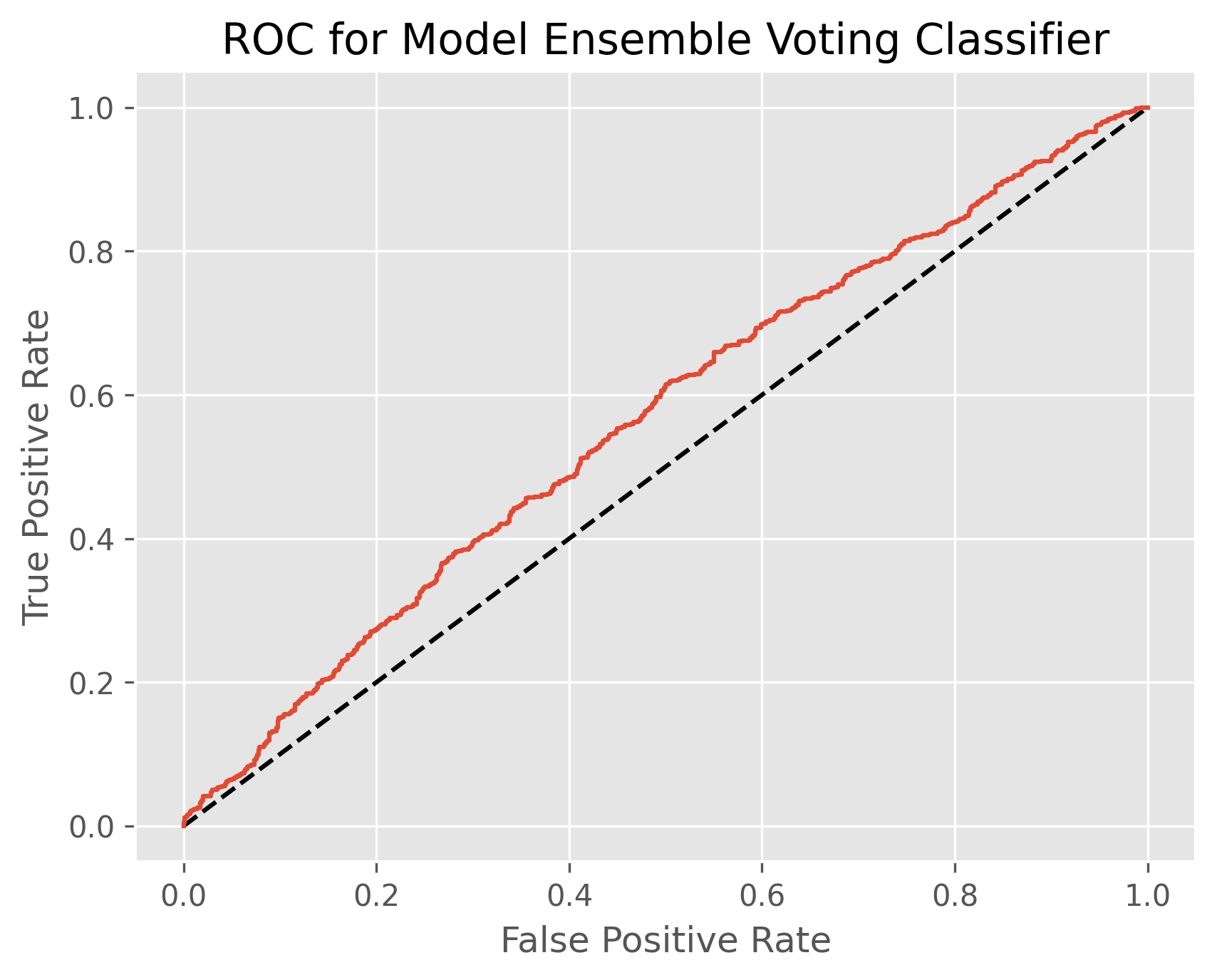
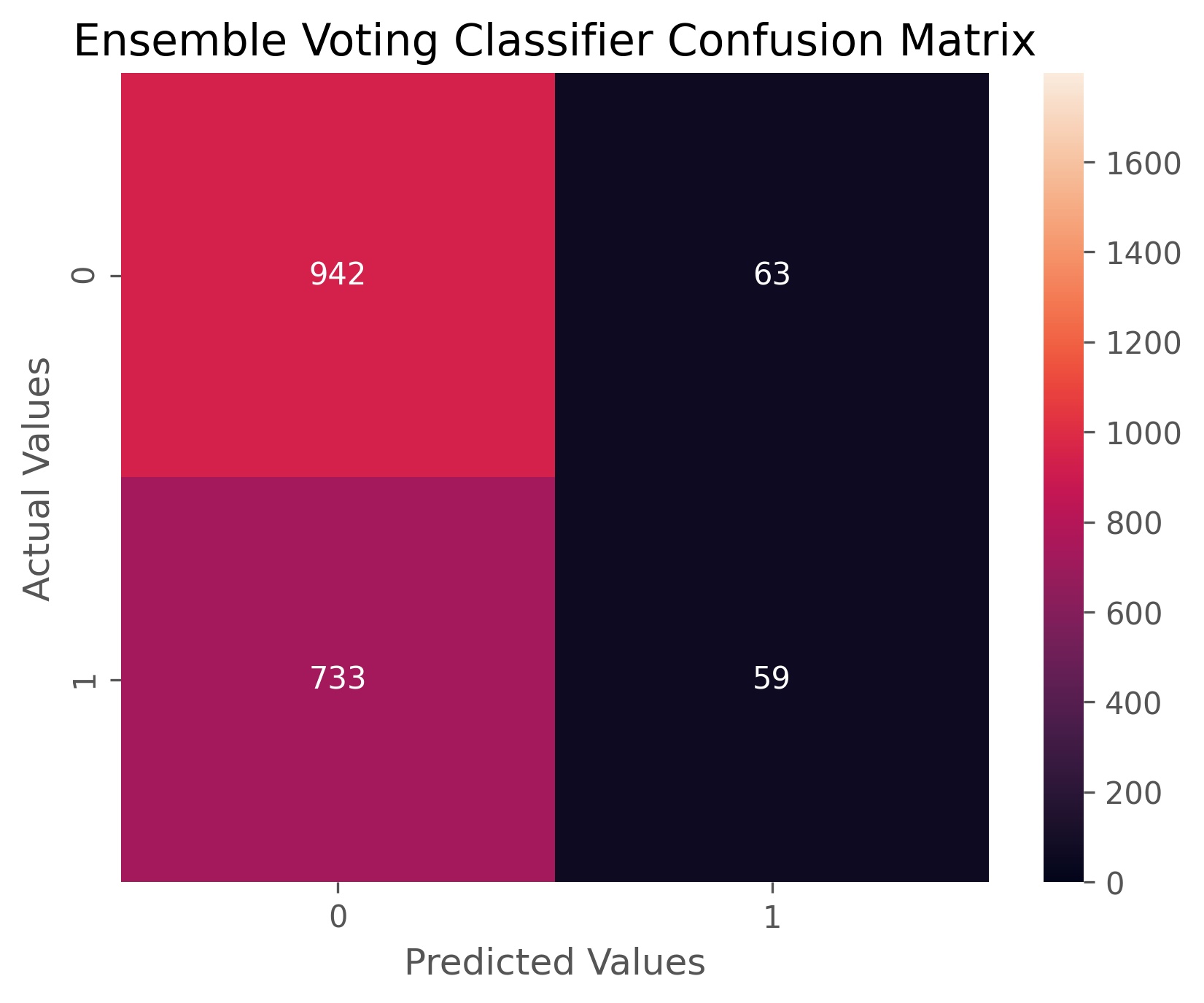
Meta-Estimator Results:
The model ensemble voting classifier achieved an accuracy score of 55.4% and an ROC AUC score of 56.5%. This model tries to find a middle ground between being effective at picking when volatility won’t go up and a model that isn’t biased against correctly picking when volatility will be high.
Actionable Insights:
Let’s be honest, this isn’t an incredibly useful model on it’s own. If someone came up to me and told me they have a little bit over a 5% edge on when volatility would go up, I don’t know if I would be racing off to scalp contracts with this information. Even our best performing individual model, the random forest, only gave us a 7% edge (and was pretty bad at correctly identifying high volatility)! That’s not to say that there isn’t an edge; all of our models fall pretty consistently around 55% accuracy.
There are also some trade-offs to using this limited data. Topics come and go pretty quickly. On one hand, the time-frame of this data is fairly early into his presidency. The model could possibly improve in predictive power as Trump spent more time in office, and possibly built more influence on the markets. On the other hand Trump is now a lame duck, and whatever influence he may have once held over the markets will probably soon wane. What is sure to continue is public influence through social media. In particular, Trump has solidified Twitter’s role as a platform through his presidency. The flame of power will be passed down through time, but for the foreseeable future it will be done on Twitter.
It is also worth noting that the aim of this project was to test investor instinct, namely that a single tweet fired off by Trump could affect market volatility. Each individual tweet was counted, where we may have gotten more predictable results had we aggregated our word counts throughout the duration of each trading day. This would be more a reflection of Trump’s general sentiment that day on Twitter rather than the sentiment contained within a single tweet.
In practice, this model would be more useful contained inside a meta-meta-estimator examining a variety of inputs in order to predict market volatility. As for investors’ anxiety surrounding Trump’s tweets: I can’t for certain say they are wrong, but there aren’t too many strong indicators that they are right. I guess half the reward for being superstitious is being able to hold an opinion with conviction while others are unsure. At the end of the day, it is probably a very good thing that we can’t reliably predict market action based on the 250 characters or less typed by one man, regardless of office. The implications of that reality would be worrisome to say the least.