But Jerome... what about inflation?
18 September 2020

Background:
It is an understatement to say that 2020 has been an unusual year for many. In addition to the loss of life due to COVID-19, the way we live our everyday lives has been affected and we don’t know when it will go back to normal. Add that uncertainty to the unknown time frame for a vaccine and we get some very scared markets. We certainly felt that volatility in March when we experienced the worst stock crash since at least 2008, with some calling this the worst since the Great Depression as the S&P 500 tumbled by nearly 30%.
There is one stark advantage of this contraction over those in the past: new tools. The Fed employed quantitative easing (including buying of junk bonds), slashed interest rates to nearly zero, and allowed immediate treasury security exchanges for cash-loans with an almost reckless abandon. Congress put aside petty party differences and whipped up a bill to provide immediate stimulus, protect the unemployed, prevent evictions, and provide small business loans. They even thought about doing it again before settling on vacation instead.
Much like the declining value of the growing number of ‘Powell make money go brrr’ memes circulating the internet, one would expect all this liquidity to boost inflation. Silver and gold prices sure seem to reflect this. I have personally experienced my Iron Condors on GLD and SLV crashing up by several standard deviations (Black Scholes model). Powell directly contradicted this in his latest speech, where he says the Fed will keep interest rates near zero until 2023 or inflation reaches 2% again.
Normally inflation is measured by percent change in the CPI. The consumer price index is a market basket that contains items an average consumer would buy. The thing is, spending has been all but average lately. Restaurants shutting down have led to an extreme demand on grocery stores. With no basis for adding floor and shelf space for what is hopefully a temporary situation, there was no choice but to drive up the price of groceries. On the other hand, items like plane tickets and used cars have their cheapest prices in years. Least to say, this has been a very confusing time for our market basket. The question that naturally arises from this is: Is the CPI accurately reporting our inflation levels with all of this turmoil?
This post aims to explore the validity of CPI in measuring current inflation, and if possible model where inflation should be.
Computing Environment:
Python 3.7.0numpy 1.19.1
pandas 1.1.0
yfinance 0.1.54
DateTime 4.3
matplotlib 3.3.1
fredapi 0.4.2
seaborn 0.10.1
requests 2.24.0
bs4 0.0.1
scikit-learn 0.23.2
Data:
Stock Market:
SPY: SPDR S&P 500 ETF Trust. 500 largest market cap weighted US common stocks based on the S&P 500 index.
Precious Metals:
SLV: iShares Silver Trust. A trust holding silver bullion that is generally valued by daily spot price of silver, less fund expenses.
GLD: SPDR Gold Shares. A trust holding gold bullion that is generally valued by the daily spot price of gold, less fund expenses.
PPLT: Aberdeen Standard Physical Platinum Shares ETF. A trust holding physical platinum that is generally valued by daily spot price of platinum, less fund expenses.
Dollar Valuation Assets:
DX-Y.NYB: US Dollar/USDX - Index - Cash. Weighted index of currencies used to measure the value of the dollar as compared to currencies of major US trading partners listed in the FOREX market. Market basket of currencies consists of the Euro, Swiss Franc, Japanese Yen, Canadian dollar, British pound, and Swedish Krona, with largest weighting towards the Euro and the least weighting given to the Swiss Franc.
TLT: iShares 20+ Year Treasury Bond ETF. An ETF that tracks the performance of US government bonds with 20 or more years until maturity. Lower Fed interest rates tend to drive up the price of the bonds.
^TNX: Treasury Yield 10 Years. An index that tracks the value of 10 year Treasury Notes.
CPI: Seasonally adjusted Consumer Price Index based on a market basket of consumer goods.
Data sourcing and cleaning:
Data for SLV, GLD, PPLT,DX-Y.NYB, TLT, ^TNX, and SPY were web scraped using the yahoo finance package. Close prices were used for each trading day. Data was merged using date as an index.
Seasonally adjusted CPI data was gathered from the St. Louis FED using the fredapi package. Data was only available for monthly intervals, so the data was subsequently resampled to daily frequency and interpolated to fill in missing values. This was then merged onto the data frame using date as an index.
In order to make a market basket for precious metals, market cap data was scraped from the yahoo finance website using the beautiful soup and requests packages. This data was converted to a float after number denominators (‘M’, and ‘B’) were removed and multiplied by the appropriate value.
Exploratory Analysis:
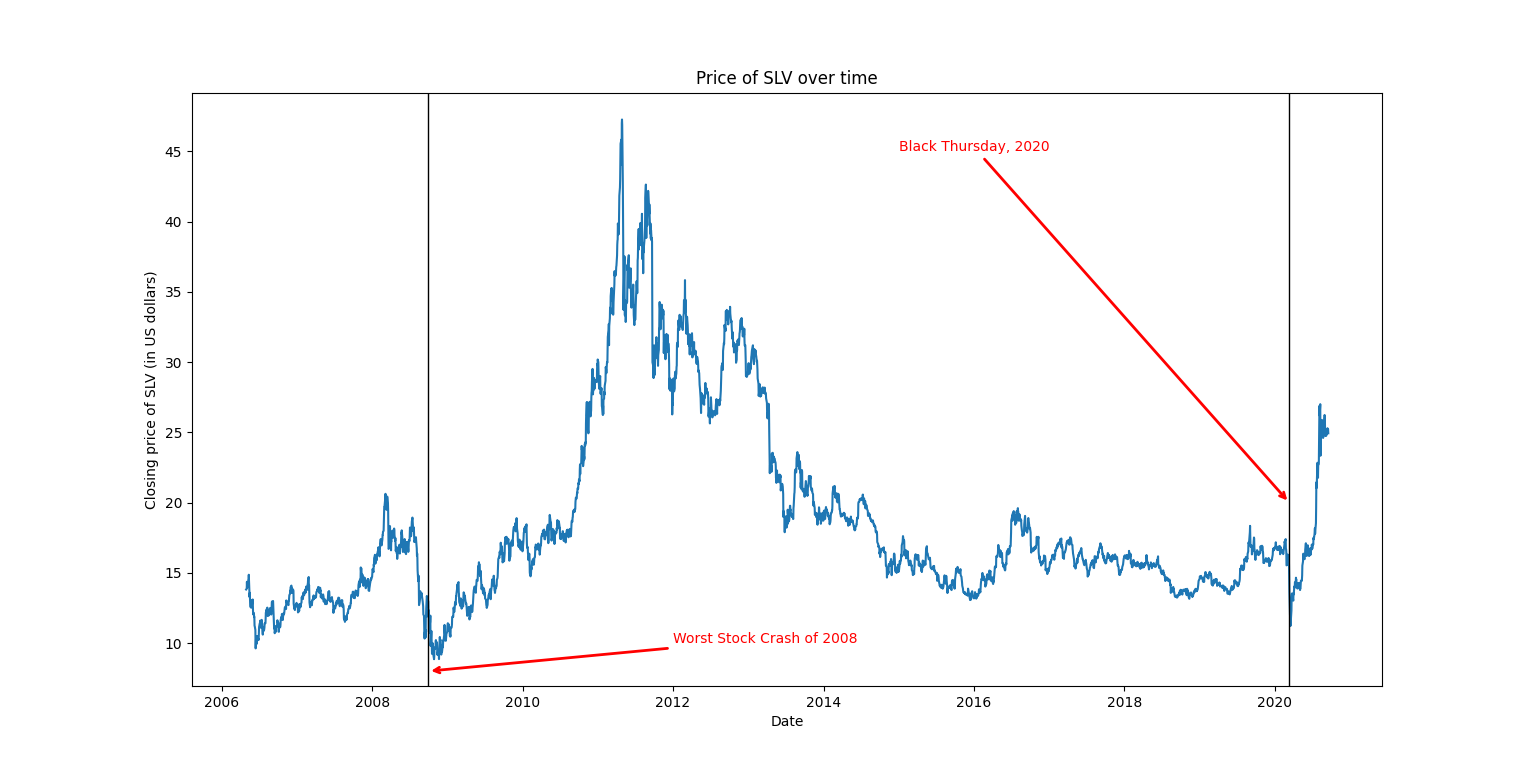
The first thing observed is that the price of silver has indeed ‘crashed up’ since the 2020 COVID-19 market turmoil. This activity looks pretty similar to what happened following the 2008 financial crisis. On both occasions the price fell sharply along with the other assets in the crash, then violently rose above pre-crisis levels. This may in part be due to precious metals traditionally being used as a hedge against inflation during times where the public sentiment thinks the general market is too risky. It is also worth noting that the price of silver steadily decreased as the market gained more bullish stability following the starting around 2012.
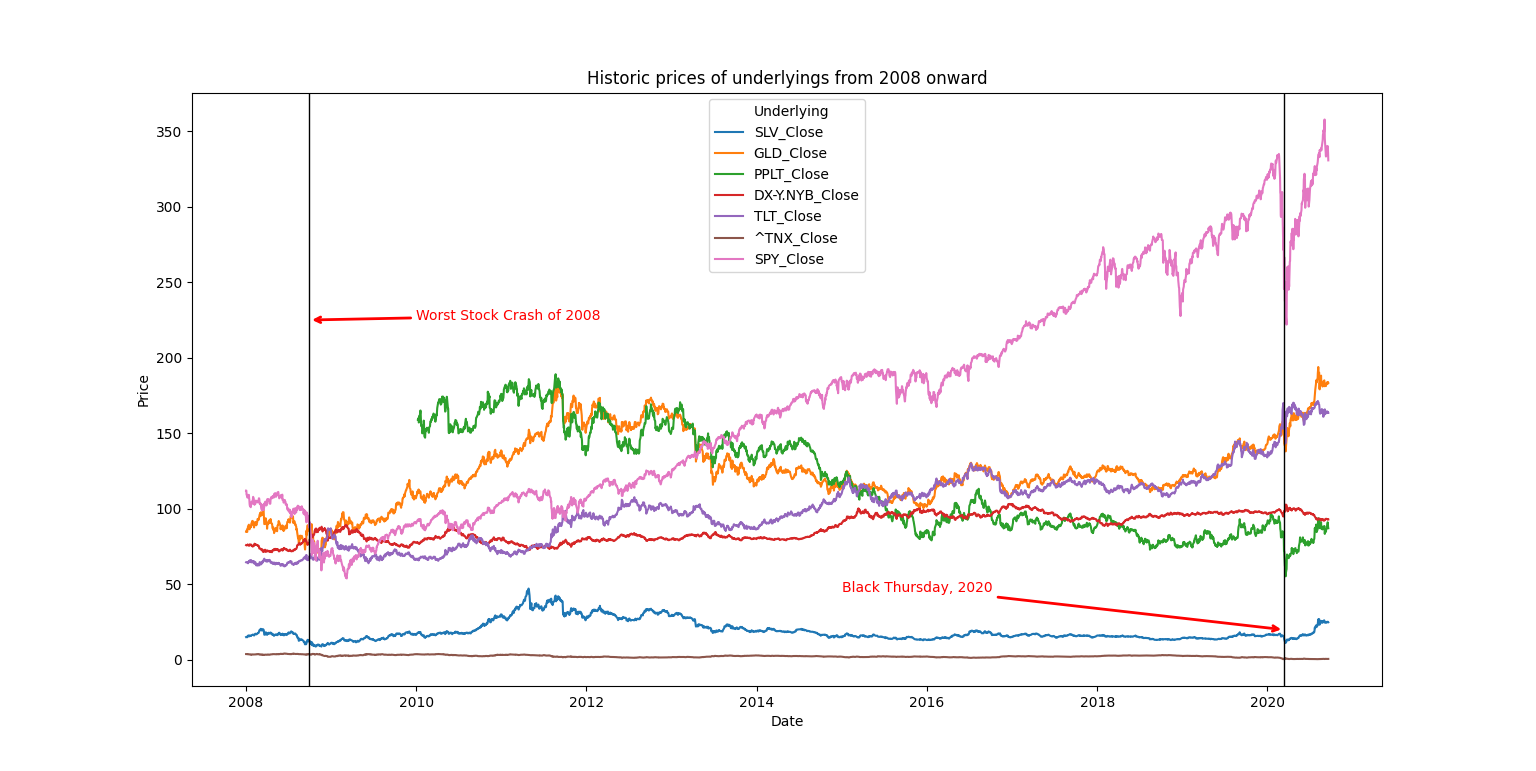
If we then look to all of our assets from 2008 through 2020 we notice the other precious metals follow suit with silver. We can also clearly see the crash and very bullish recovery of the S&P 500. This appears somewhere between non-correlated and negatively correlated to the activity of the precious metals. The value of the dollar against other currencies has steadily risen since the 2008 crash until the fallout seen in March of 2020.
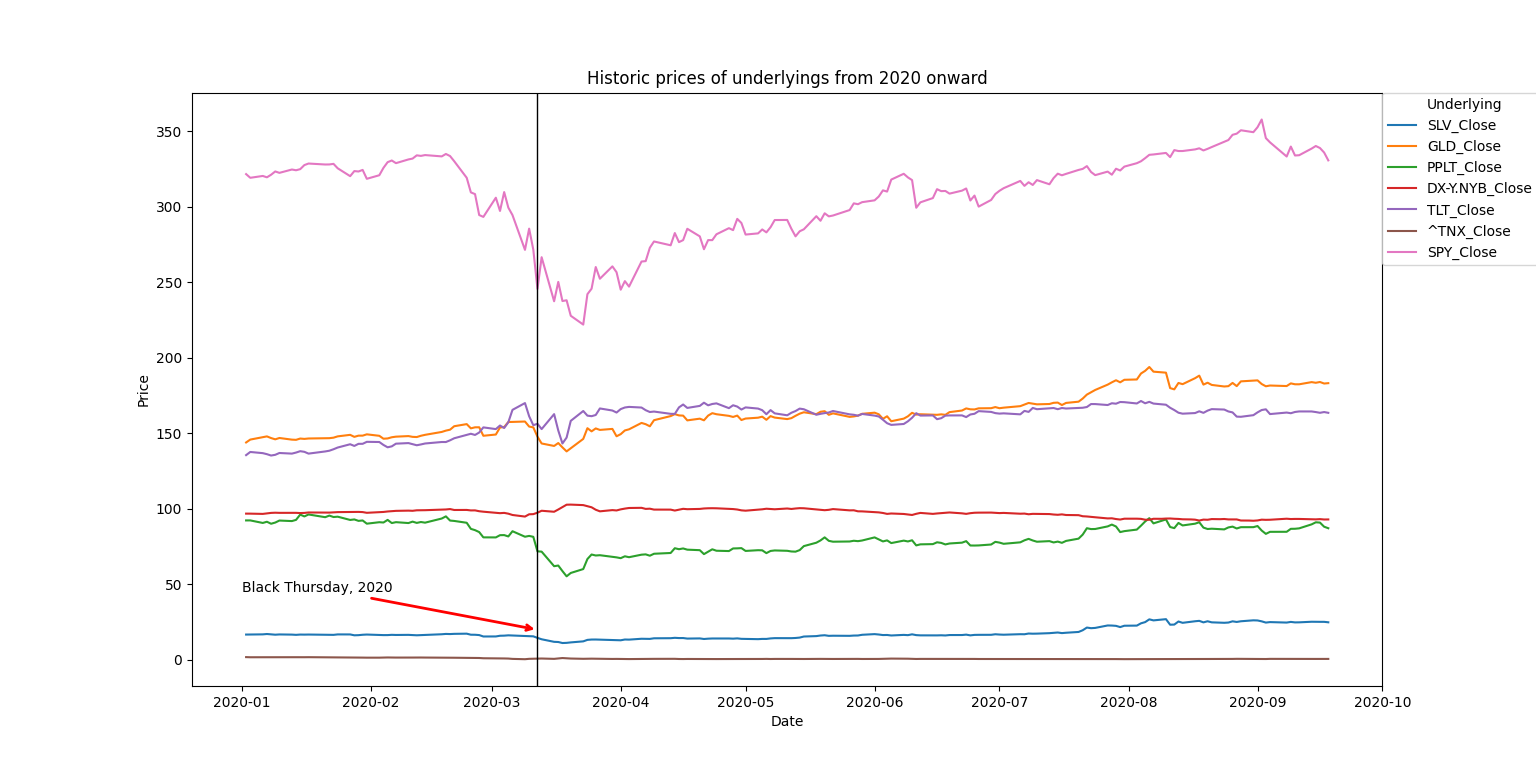
If we focus on just 2020 we can see this low to negative correlation between precious metals and the S&P 500 has reversed and they all seem to be tracking together through ups and downs.
Appearances can be deceiving, and these line plots don’t generally scale well when comparing assets with a wide range of volatility (S&P 500) to those with a lower range (bonds, treasury notes, and dollar valuation). To do a quick sanity check, weekly percent changes in price movement were calculated amongst the assets. Wednesdays were chosen as a reference point as they are less likely to be holidays.

The distribution of weekly percent changes from 2008 forward were first compared side by side in bee swarm plots to avoid binning bias. It seems that while distribution is fairly even among the assets, precious metals had a higher amount of extreme negative outliers. Treasury notes seem to have the most extreme moves in both directions.

If we repeat this analysis for just 2020, it reaffirms our thoughts from our line plots. Most assets have some extreme negative outliers, but are generally skewed to the upside, with the exception of treasury notes and dollar valuation.
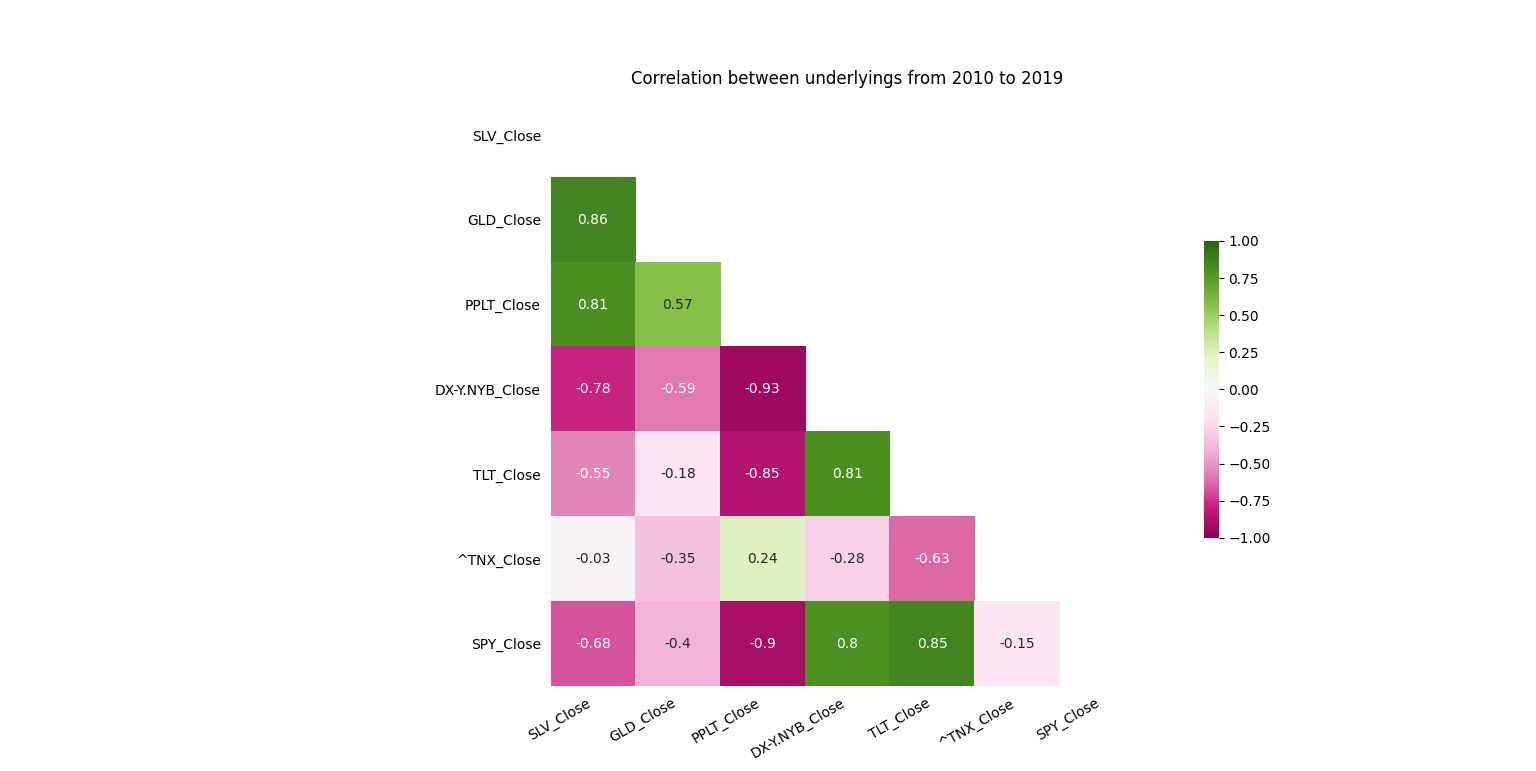
Now came the time to measure our intuition on these correlations. After dropping all missing data, this left us with a first date range from 2010 up to 2020 (PPLT did not exist until 2010). If we look at this first heatmap, SPY is generally negatively correlated to prices of the precious metals, and positively correlated to dollar valuation and bonds. The precious metals tend to be most strongly correlated amongst themselves.
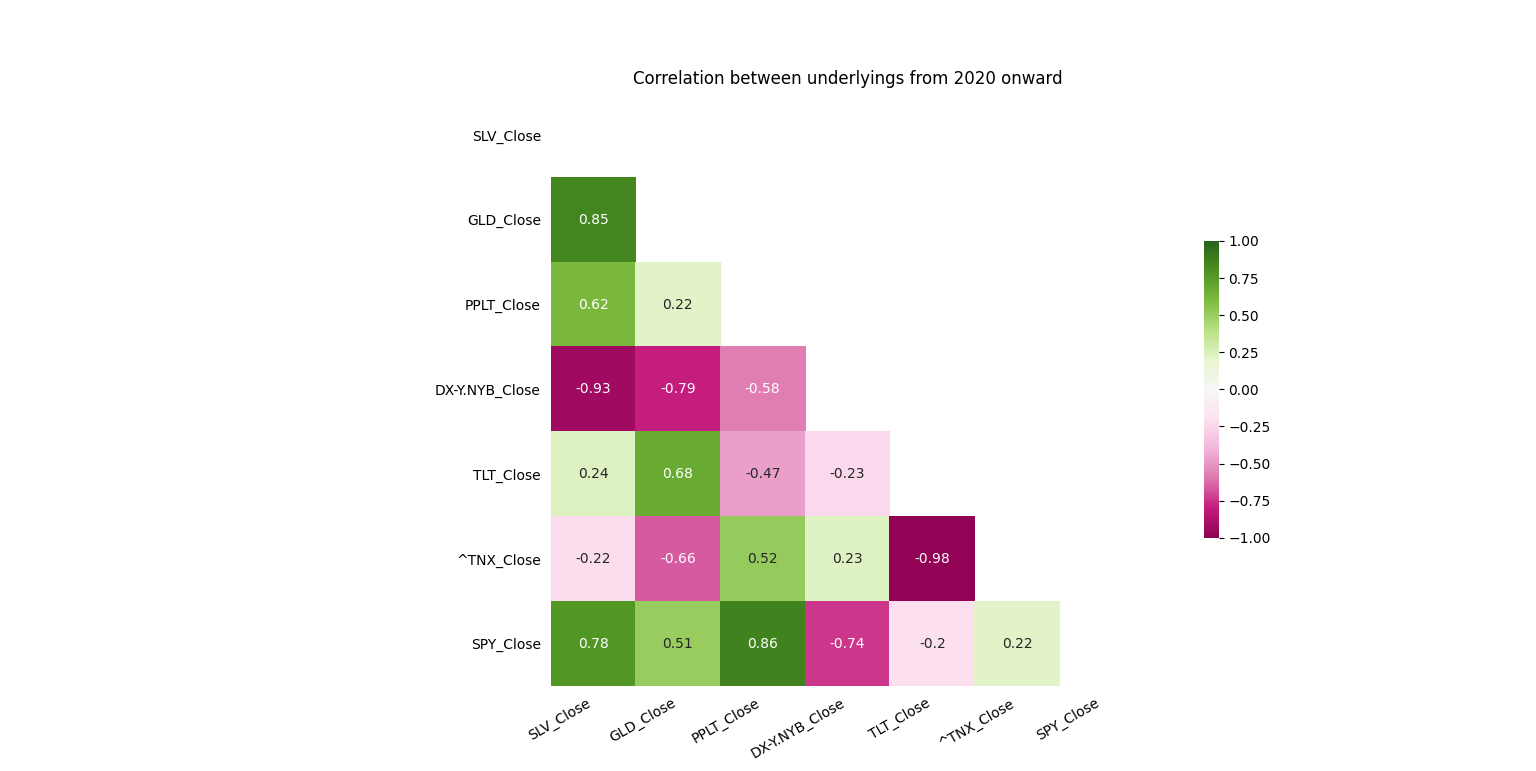
If we shift our focus to 2020, we can see that all of our relationships have practically reversed!

Next I decided to facet heatmaps for each month of 2020 through August. We can see that our relationships seem comparable to those in the 2010-2019 heatmap during January, start to change in February, and snap in reverse in March, with the strongest month in July.
Bootstrap Analysis of CPI to Precious Metals Basket
In order to perform a bootstrap analysis of the correlation of our precious metals to seasonally adjusted CPI, we first had to construct a market basket of our precious metals. This was done by fetching the last market cap value for SLV, GLD, and PPLT ($8,880,000,000, $66,990,000,000, and $741,330,000 respectively) and weighting them accordingly (~11.59%, ~87.44%, and ~0.97% respectively). The prices of each of these assets was then multiplied by their weighting for each non-missing value day (roughly 2010 to present) and summed to create the price of our new metals basket variable. The new data frame containing CPI and our metals basket was then split into data before 2020 and from 2020 forward.
We then used this information to calculate our empirical correlation between the metals basket and CPI for before and after 2020. The time frame before 2020 yielded a correlation of -0.3090621543720819. The correlation for 2020 data was 0.15357846299675024.
Just because we have a notable difference in correlation between these two time frames does not make them statistically significant. In order to check this I performed pairwise bootstrap replicates for each time frame. If we consider the empirical correlations we took to be the product of random sampling, then constructing a new array of randomly chosen pairs of our metals basket and CPI should give us a synthetic replicate of another random sample. If we do this many times, we can construct a distribution of our replicate correlations, and see if our empirical correlation falls somewhere near the mean. I formed 100,000 bootstrapped pair replicate samples for each time frame, calculated their corresponding correlations, and graphed them in a histogram against their empirical correlation along with the 95 percent confidence intervals.

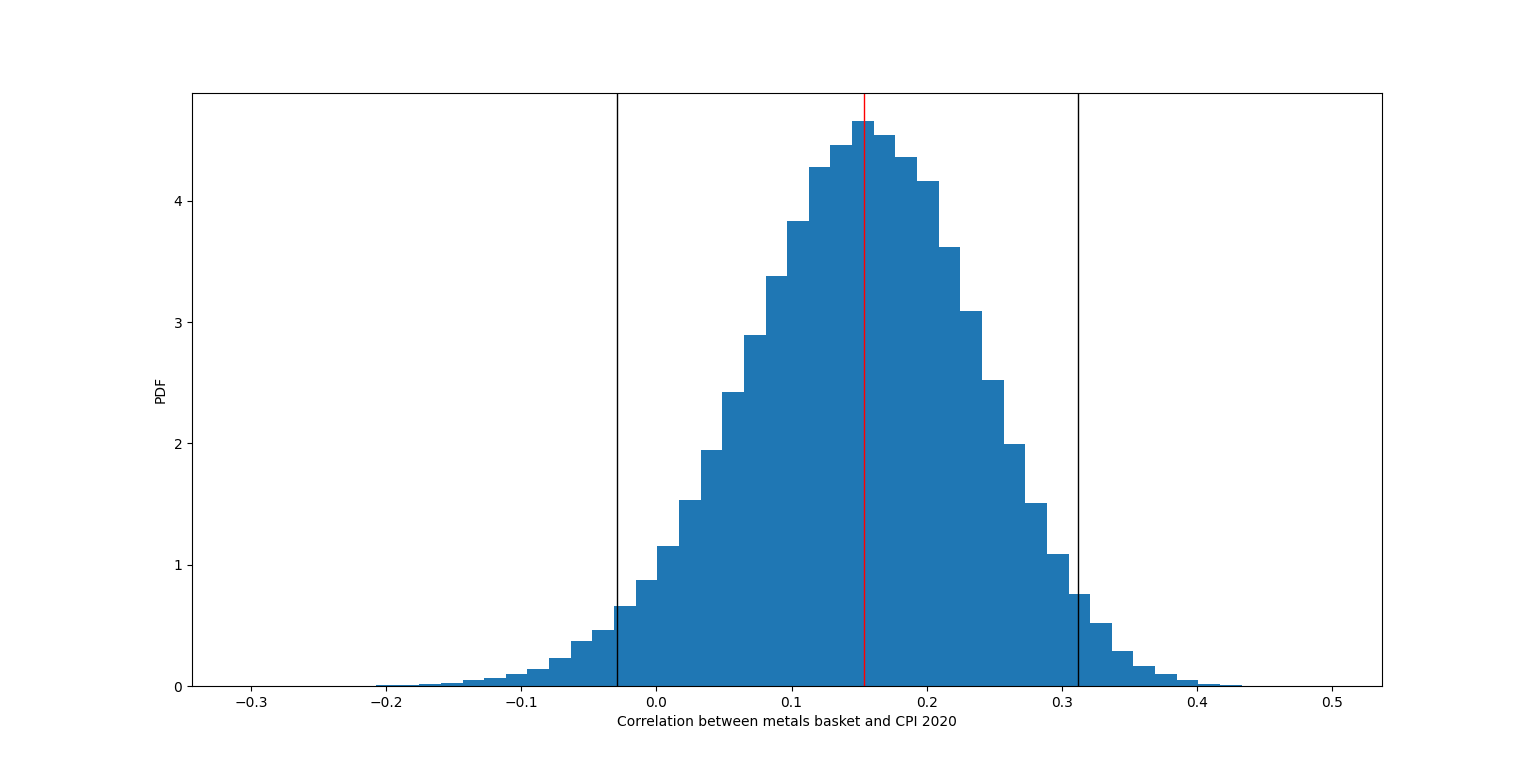
The empirical correlation looks like it falls pretty close to the mean for both time frames, indicating that our correlations are likely to be accurate representations of the relationship between the metals basket and CPI for our respective timeframes, and serves as a healthy sanity check. However, this still doesn’t answer our real question: Is the difference in relation significantly different for these two time periods? Our null hypothesis in this case is that our random sample is not significantly different from any random sample, so a relatively high percentage of our bootstrapped samples should have at least as high of a difference in correlation as our empirical difference in correlation. Our difference in empirical correlations that we calculated before from the two time frames is 0.4626406173688321 (0.15357846299675024 minus -0.3090621543720819).

As the graph above illustrates, our p-value is 0.4975. Simply put, this means that at least 49.75% of randomly generated samples for these two time frames exhibited a difference in correlation as high or higher than our empirical difference. Given this high p-value, we fail to reject the null hypothesis that our empirical difference in correlation is representative as any random sampling. This means that our difference in correlation is statistically significant, or that these observed differences in relationship have a high probability of carrying some real meaning!
Elastic-Net Linear Regression
Now that we have a basis for building our model, let’s try to calculate what we have been waiting for: What is the CPI as indicated by our assets? To do this we will fit an Elastic-Net linear regression model to our data, but first let’s explore what this means.
In a normal linear regression we select our variables, and receive p-values of their statistical significance. We can instead use a LASSO model to deselect variables that aren’t important in our equation based on a given alpha parameter (think of a cowboy lassoing off the weaker cattle in a herd). Ridge models solve this problem of significance by decreasing the coefficient weighting of each variable for a given alpha (think of climbing to the top of a ridge, getting cold, and as a result... things start shrinking). Much like Miley Cyrus, we desire the best of both worlds. Enter our protagonist: Elastic-Net. Elastic-Net models use two parameters, lambda-1 and lambda-2, to make the model act more like a LASSO model (lambda-1), a Ridge model (lambda-2), or a combination of both to fit a model with the lowest mean squared error.
To prep our data, we split our data frame into two groups: before and after 2020. Once we fit our model and validate it we will use it to predict the value of CPI for our 2020 data. We split our variables into dependent (CPI) as a data frame as y, and independent (all other variables, including date) as x. To prevent overfitting of our model, we randomly split our pre-2020 data into a model training group (70%) and a model testing group (30%) to measure our validity. We then create a parameter grid with all possible values for alpha and our lambda-1 to lambda-2 ratio. We use grid search cross-validation with 5-fold cross-validation and fit our training data in order to perform hyper-parameter tuning for our model. We then use our test data to predict CPI values and score our model based on how our predicted CPI models measure up to our test data CPI values.
The results for our hyperparameter tuning show a model of best fit with alpha of 0.001 and a lambda-1 to lambda-2 ratio of 0. To clarify, a lambda-1 to lambda-2 ratio of zero essentially means we have constructed a Ridge model and also means that our variables were all significant given weighting. The R-squared value for our tuned model is 0.9929669353670906. This means the model was able to explain ~99.3% of the variance in our CPI values. The mean squared error for our model was 0.7974450384473997, a relatively low value.
Results:
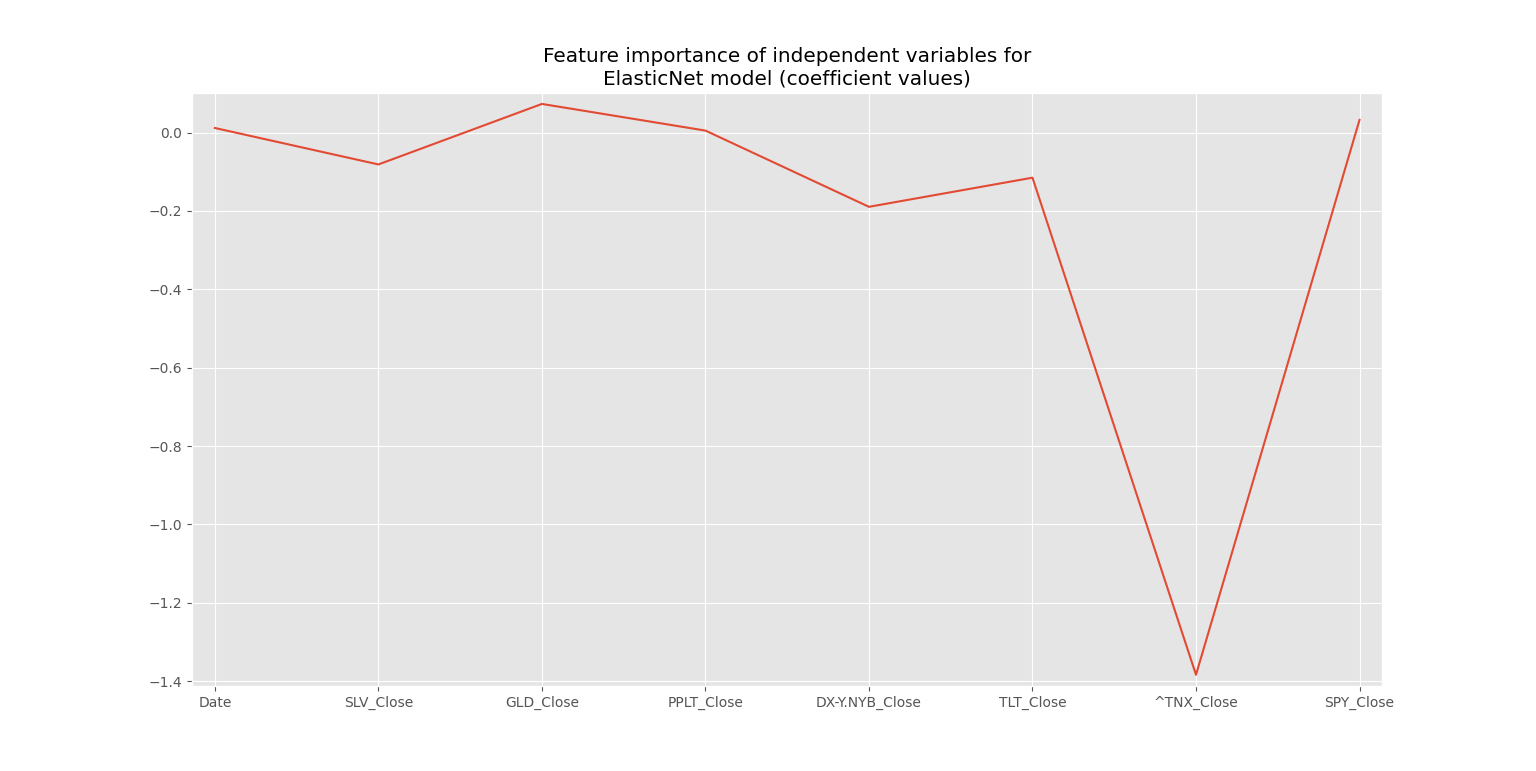
When we look at our feature significance, we can see that the 10 year treasury note is our strongest indicator of CPI. Next comes DX-Y.NYB, the dollar valuation against other currencies. This may seem intuitive as the dollar value is affected by inflation, but each country’s own rate of inflation also affects the value of the market basket the dollar is valued against. Third comes treasury bonds. These three variables all exhibit a negative correlation, going down in value when CPI rises. Gold does the opposite, and goes up in price as inflation increases as one would expect. What is surprising here is silver’s negative relationship to inflation (although slight).
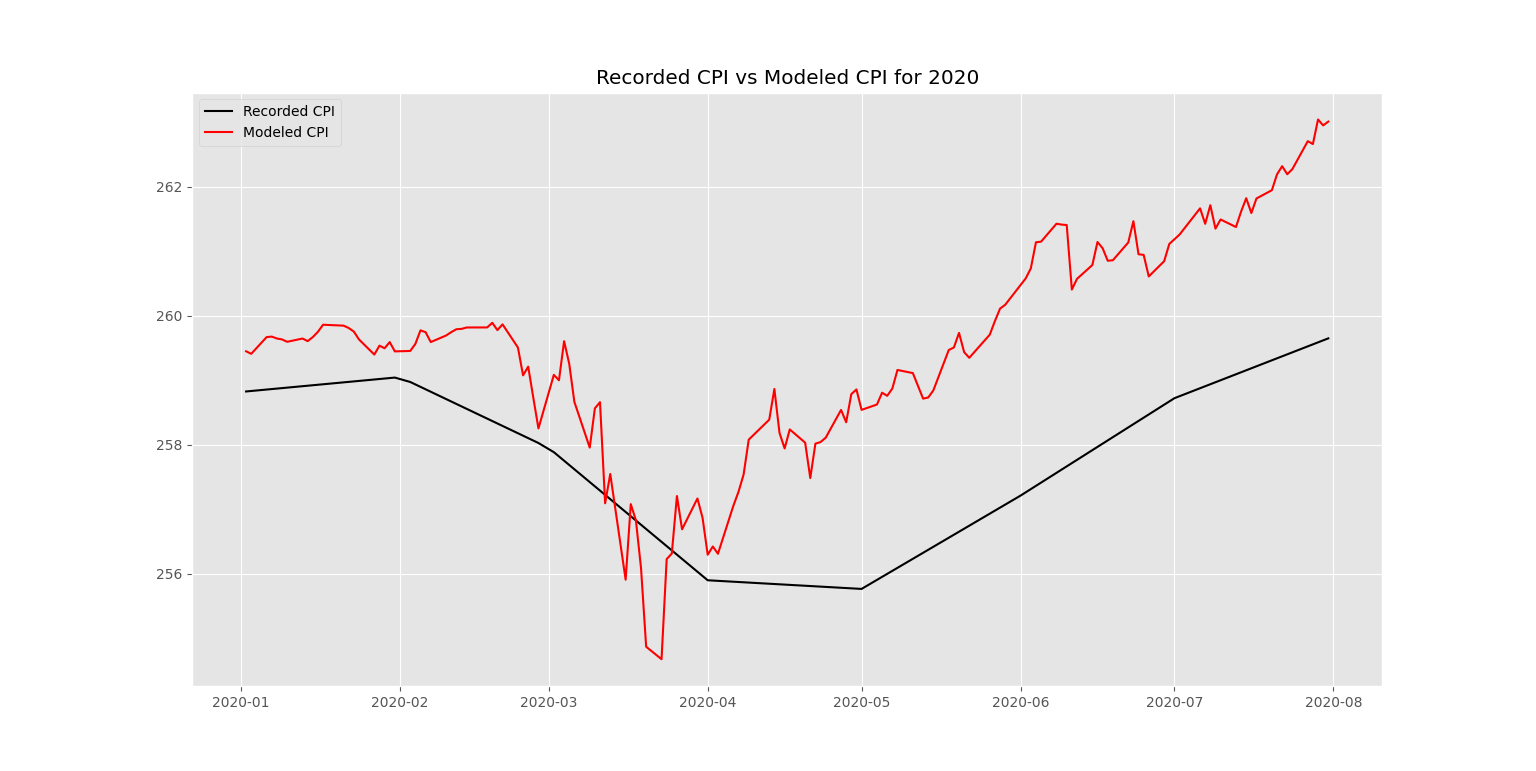
When we fit the model to our 2020 data, we see that our CPI value is quite different than what was recorded. It declines steeper and faster than the recorded CPI and recovers much faster as well. It is interesting to note that this quick boost from lows in inflation happened around the same time the Fed took measures to introduce liquidity into the market (late March/early April 2020).
We can now use the modeled CPI to calculate year-over-year inflation rates. Recorded CPI for July 31st, 2020 is $259.65009677, while our modeled price is $263.00900178. Using our CPI price from July 31st, 2019 ($256.294), we can calculate our year-over-year inflation through a simple percent change formula. Our recorded CPI indicates a year-over-year inflation rate of 1.30947146% as of July 31st, 2020. However, our modeled CPI indicates an inflation rate of 2.62003862%!
Actionable Insights:
Our model indicates a much higher inflation rate than Powell seems to acknowledge by his actions, but what does that mean for us? To me this speaks of two possible scenarios.
In the first, inflation is high and may shoot higher. This means that now may be a pretty good time to have debt, as it is inflation protected to some extent. I want to clarify before you run off and charge a Lamborghini to your credit card that I mean good debt, not bad debt. Please don’t buy a Lamborghini. Conversely, now may be a pretty bad time to be a lender.
First scenario aside, let’s talk about a different and more ominous one, and one that I personally believe to be more likely. Jerome Powell has a ton of analytical tools at his fingertips, and we must assume him to be a good actor. In that case, these efforts to inject even more liquidity into the economy may signal that he believes there may be A) another crash(es), B) a prolonged recovery, or C) both. We may be in for a bumpy few years before we get to ride the bull again.
Github Link Here
Note: if you want to run this script, you will need to register a FRED API key (it's free!). Once you receive your API key, save it to a file, and replace the appropriate filepath for that variable in the script.
Special Thanks:
Matthew McMahon, PhD - Assistant Professor of Economics, University of Arkansas Little Rock
Jason Xiong, PhD - Assistant Professor Department of Computer Information Systems, Appalachian State University
Brandy Hadley, PhD - Assistant Professor Department of Finance, Banking and Insurance, Appalachian State University
Joseph Cazier, PhD, CISSP & CAP - Professor Department of Computer Information Systems, Appalachian State University